GSL・VisualC++・OpenGLによる仮想物理実験室
円形膜(太鼓)の振動
近年のパソコンの凄まじい発展は、安価に手軽に入手できる汎用パソコンで物理シミュレーションを可能としました。
一方、物理シミュレーションに必要不可欠な計算アルゴリズムも整備され、簡単に目的の計算を行える環境が整ってきました。
つまり、これまでは物理学の専門家以外には非常に敷居の高かった物理シミュレーションが、誰にでも簡単に行える時代が到来していることを意味しています。
さらに、昨今の物理学の進展に伴なって研究領域に到達するまでに習得する必要となる概念が非常に多くなってきている物理学を志す者にとっても、効率的に学習する上で非常に有用となります。
そこで本稿では、無料で利用できるC++言語の開発環境として「Microsoft Visual C++ 2010 Express」、科学計算ライブラリとして「GSL(GNU Scientific Library)」、描画には OpenGL(+GLSL) を用いて、「仮想物理実験室」を構築します。
題材としては、円形膜(太鼓)の振動を取り上げ、
物理学で非常によく出くわす、(1)「ヘルムホルツ方程式」、(2)「極座標形式」、(3)「関数の直交性と完全性」、(4)「境界条件」、(5)「初期条件」
などの概念の理解を目的とします。最終的には基準振動だけでなく、任意の膜の形状(初期条件)に対する時間発展の計算までを行います。
本稿は初めて物理シミュレーションする方を対象に、GSLの導入から数値計算までの実行手順、計算結果を3次元グラフィックとして出力するまでのOpenGLの使い方までの一連の流れを体感できる内容となっています。このような概念の習得は物理シミュレーションに留まらず、昨今著しい発展をみるゲームプログラミングや画像処理といったコンピュータ・グラフィックの分野でも、今後重要になってくると考えられます。
多くの方の学習の一助になることを願っています。
本稿について(HTML5 を利用したデジタルコンテンツ)
本稿はウェブページ記述言語 HTML の最新バージョンである HTML5 と Javascript で作成してます。
HTML5 ではウェブブラウザ上で自在に描画するための canvas 要素と呼ばれる領域が標準で用意されており、ピクセル単位の描画を Javascript で制御することができるため、例えば物理現象の時間発展を時間ステップごとに描画することができます。
これは、数値計算結果のグラフだけしか掲載することができなかった従来の紙ベースの書籍に対して、読者により直感的な理解を可能とする表現の可能性を秘めていると考えられます。
本稿は、ウェブブラウザで閲覧可能なスライド形式型の HTML5文書です。
HTML5 はWeb標準を謳っておりますが、2012年10月時点では草案段階で、ウェブブラウザでの実装はまだ不十分な状況なため、本稿が著者の意図どおり動作するブラウザは HTML5 に先駆的なGoogleChrome と Mozilla Firefox のみとなります。本稿は上記ブラウザの最新バージョンのみをサポート対象とします。
本稿は、次世代の技術である HTML5 を積極的に取り入れた実験的コンテンツとしての位置付けもあります。
例えばこれまではプレゼンソフトとしてウィンドウズ社製のパワーポイントがデファクトスタンダードの地位を占めていますが、HTML5 がもつ汎用性はその牙城を崩すポテンシャルを持っているように感じます。
いずれにせよ、本稿では HTML5 の機能を積極的に利用します。
本稿で利用ライブラリ
本稿では以下のJavascript ライブラリを利用させていただいております。 この場にて勝手に御礼申し上げます。
- ■スライド作成:html5slides
- ■インターフェース:jQuery
GSL・VisualC++・OpenGLによる仮想物理実験室1
「円形膜(太鼓)の振動」の内容
本稿の目的は「科学計算ライブラリ「GSL」を利用した円形膜(太鼓)振動の時間発展シミュレーション」です。 任意の初期条件に対する円形膜の時間発展を計算するために必要な事項について順を追って説明します。
計算例:任意の初期条件に対する円形膜の時間発展(中心から離れた場所を叩いた場合)
以下の動画は、本稿で取り扱う計算の一例です。
本稿の流れ
1.物理系の理解と円形膜の振動の時間発展の計算
本稿では、円形膜が従う方程式の導出から、ヘルムホルツ方程式の導出、第一種ベッセル関数の解説(直交性・完全性)、境界条件の与え方などを順を追って解説します。 さらに、円形膜の基準振動から任意の初期条件に対する膜振動の時間発展をGSLを用いて実際に計算します。
2.仮想物理実験室の構築(GSL、OpenGLの環境設定)
本稿は、マイクロソフト社が無料で提供している統合開発環境「VisualC++ 2010 Express」に科学計算ライブラリ「GSL(GNU Scientific Library)」と、コンピュータ・グラッフィックの標準技術である「OpenGL」を用いて、仮想物理実験室を構築します。 GSL(GNU Scientific Library)は、計算物理の専門家集団によって C言語で記述された科学計算ライブラリで、GNU ライセンスで公開されています。 GSL のセットアップから基本的な使い方を順を追って説明します。
3.OpenGLを用いて計算結果を描画
C言語で OpenGLを利用する際に非常に便利なライブラリ「OpenGL Utility Toolkit(GLUT)」を用います。 OpenGL の基本的な使い方から、円形膜の描画まで順を追って解説します。 数値計算で得られた結果を用いて円形膜の時間発展を描画します。
本稿の目次
- ・ はじめに
- 1.円形膜(太鼓)の物理
- 2.GSLを利用した数値計算
- 3.OpenGLによる基準振動のアニメーション
- 4.任意の初期条件に対する円形膜のシミュレーション
- ・ 最後に
一部、WebGL を用いて描画しています。そのため、WebGLが描画可能なブラウザ(GoogleCrome や Firefox)でご覧頂く必要があります。
付属の C++言語 プログラムソース
本稿では、C++言語で計算した数値データを HTML5 + Javascript + WebGL で描画しています。 本稿で取り扱ったシミュレーションのすべてのC++言語プログラムソースが付属されています。 個人利用のための改変などはご自由に行うことができますので、様々な系にてシミュレーションを行なってみてください。 興味深いシミュレーション結果が得られた際には是非ご連絡ください。本ウェブサイト上で紹介させて頂きます。
- ・第一種ベッセル関数の計算.cpp
- ・第一種ベッセル関数のゼロ点探索.cpp
- ・円形膜の基準振動の空間分布(t=0).cpp
- ・OpeGLの動作確認(立方体).cpp
- ・円形膜の描画.cpp
- ・円形膜の基準振動アニメーション.cpp
- ・二重適応型積分のサンプルプログラム.cpp
- ・三角関数の直交性の確認.cpp
- ・第一種ベッセル関数の直交性の確認.cpp
- ・三角関数による任意の関数の展開.cpp
- ・第一種ベッセル関数による任意の関数の展開.cpp
- ・2重積分のサンプルプログラム(モンテカルロ積分).cpp
- ・任意の初期状態に対する円形膜の時間発展_GLUT.cpp
本コンテンツ販売について
| 販売形態 | ダウンロード |
| 価格 | 2,100円(税込) |
| 決済方法 |
■ 銀行振込 【取引銀行】七十七銀行 本店営業部 【口座番号】7732899 【口座名義】特定非営利活動法人 natural science (トクヒ ナチュラルサイエンス) ※振込手数料お客様負担となります |
| 購入手順 | info@natural-science.or.jpに購入希望の旨をお知らせください。 入金の確認後、メールにて本コンテンツの詳細をお送りいたします。 |
- ・本コンテンツに対するご意見・ご質問・ご指摘がございましたら、お気軽にお問い合わせいただければと存じます。著者の答えられる範囲でお応えいたします。
- ・問い合わせいただいた内容を踏まえて、加筆訂正は随時行います。購入者はいつでも最新バージョンのコンテンツをご覧になることができます。
- ・本コンテンツ並びにプログラムソースの著作権は著者が保有しております。転載などの際には必ず著者の許可が必要となります。
- ・購入後の返品は、本コンテンツの性質上受けかねますことをご了承ください。
本コンテンツのイントロダクション
本コンテンツのイントロダクション部を公開します。購入の参考にしてください。
※閲覧には HTML5 先駆的なGoogleChrome と Mozilla Firefox でご覧ください。
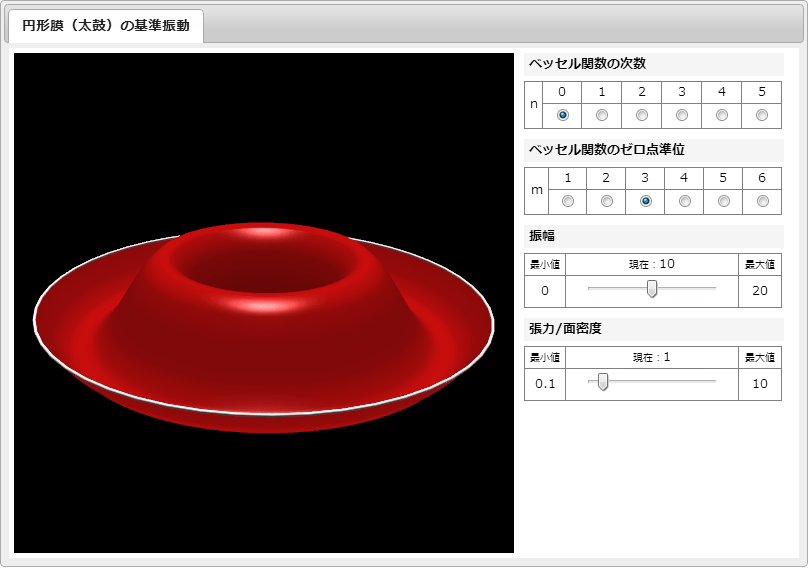
蛇足:HTML5 + WebGL を用いた「円形膜(太鼓)の基準振動ビューア」
本稿で取り扱う、第一種ベッセル関数による円形膜の基準振動を視覚的に理解すること目的とした HTML5 + WebGL にて作成されたビューアを公開します。