「physics.js」による仮想物理実験室の構築:等加速度運動
文責:遠藤理平
公開日:2015年02月03日
最終更新日:2015年02月03日
「physics.js」は、ウェブブラウザ内に仮想物理実験室を構築し、物理シミュレーション(数値計算+3次元グラフィックス+2次元グラフ)を実行するためのHTML5フレームワークです。 様々な物理系に対するphysics.jsを用いて作成した仮想物理実験室のサンプルを紹介していきます。今回のテーマは重力場中の等加速度運動です。
サンプル:等加速度運動
サンプル:physics.jsによる仮想物理実験室:等加速度運動
-z軸方向に重力加速度が加わる球体の運動。 x軸方向に初速度0, 2, 4, 6, 8, 10 [m/s]を与えた時の等加速度運動を行う球体の運動のシミュレーション。 0.125 [s]毎にストロボを設定。
「physics.js」で生成した動画(等加速度運動)
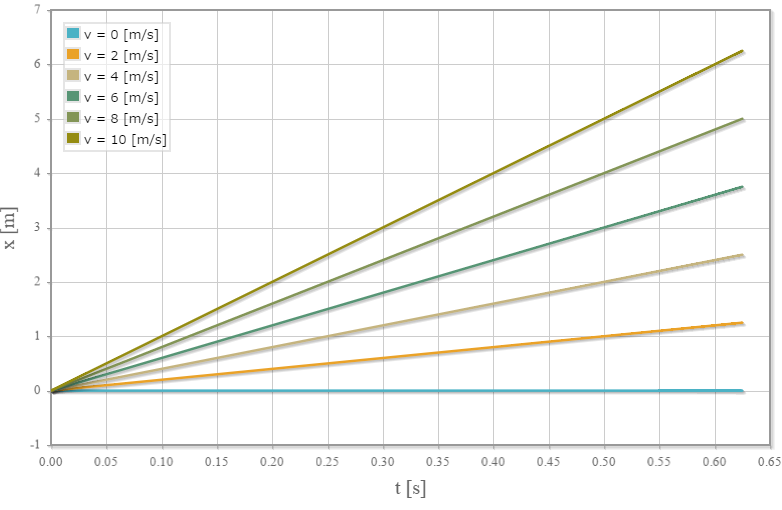
時刻vs位置x成分のグラフ
時刻 $t$[s] の位置x成分を $x(t)$[m]、x軸方向の初速度を$v_x$[m/s]と表した場合、時刻と位置の関係は $ x(t) = v_x t $ となり、等速直線運動となります。 これは、重力加速度がz成分しか持たないため、速度のx成分への影響がないためです。 上記グラフの横軸が時刻($t$)、縦軸が位置$x(t)$なので、傾きが速度 $v_x$[m/s]となります。
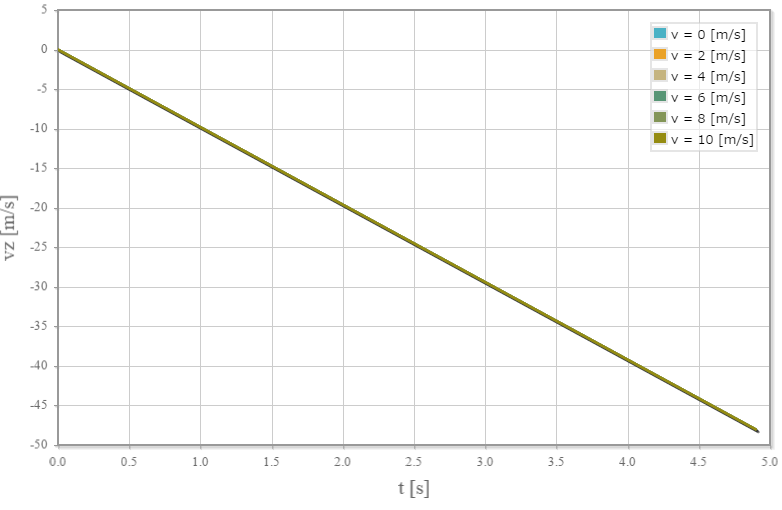
時刻vs速度z成分のグラフ
時刻 $t$[s] の速度のz成分を $v_z(t)$[m/s]とした場合、時刻と速度の関係は $ v_z(t) = - g t $ となり、時刻に対して比例関係となります。 上記グラフの横軸が時刻($t$)、縦軸が速度$v_z(t)$で、比例定数が $- g$ です。
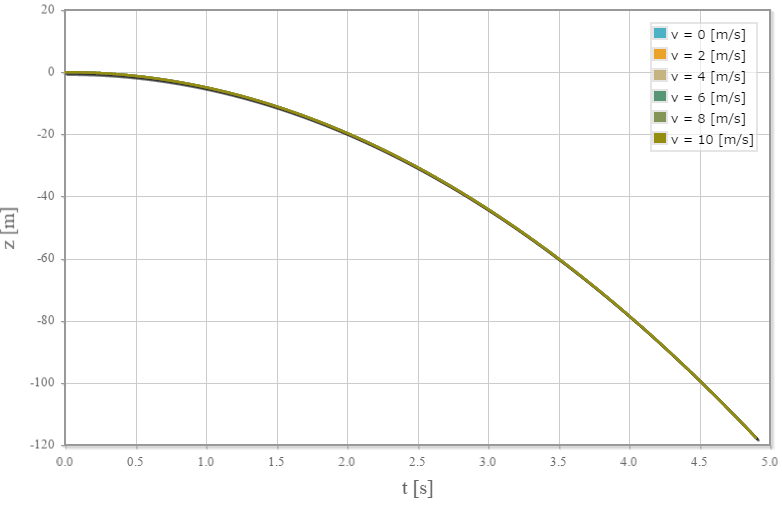
時刻vs位置z成分のグラフ
時刻 $t$[s] の位置z成分を $z(t)$[m]とした場合、時刻と位置の関係は $ z(t) = -\frac{1}{2} g t^2 $ となり、時刻に対して2次関数となります。 上記グラフの横軸が時刻($t$)、縦軸が位置$z(t)$で、2次の係数が $-\frac{1}{2} g$ です。