「physics.js」による仮想物理実験室の構築:ばねの自然長が存在する単振動+重力
文責:遠藤理平
公開日:2015年02月09日
最終更新日:2015年02月09日
「physics.js」は、ウェブブラウザ内に仮想物理実験室を構築し、物理シミュレーション(数値計算+3次元グラフィックス+2次元グラフ)を実行するためのHTML5フレームワークです。 様々な物理系に対するphysics.jsを用いて作成した仮想物理実験室のサンプルを紹介していきます。今回のテーマはばねの自然長が存在する単振動+重力です。
サンプル:ばねの自然長が存在する単振動
サンプル:physics.jsによる仮想物理実験室:ばねの自然長が存在する単振動+重力
ばね定数 $k = 5$ [N/s]のばね(自然長3[m])に質量 $m = 1$ [kg]の球体を接続。ばねの長さが自然長より1, 3, 5[m]伸びた状態からスタートします。
「physics.js」で生成した動画(ばねの自然長が存在する単振動+重力)
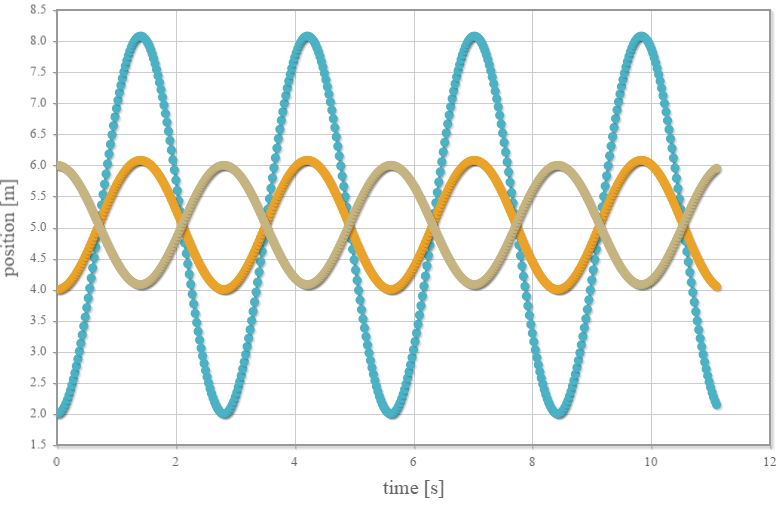
時刻vs位置のグラフ
時刻 $t$[s] の球体の位置を $z(t)$[m]と表した場合、時刻と位置の関係は $ z(t) = L \cos( \omega t + \delta) $ となります。 ただし、$L$は初期状態のばねの伸び、$\omega$は角振動数を表し、ばね定数$k$と質量$m$を用いて$ \omega = \sqrt{\frac{k}{m}} $[rad/s]と与えられ、$\delta$は球体の初期位置(z成分)が釣り合いの位置よりも上の場合には0、下の場合には$\pi$をとります(逆位相)。 上記のグラフからもわかるとおり、角振動数は初期位置に依らず$\omega = \sqrt{5}$[rad/s]なので、周期が同じ$ 2\pi/\sqrt{5} \simeq 2.81 $秒の単振動であることが確認できます。
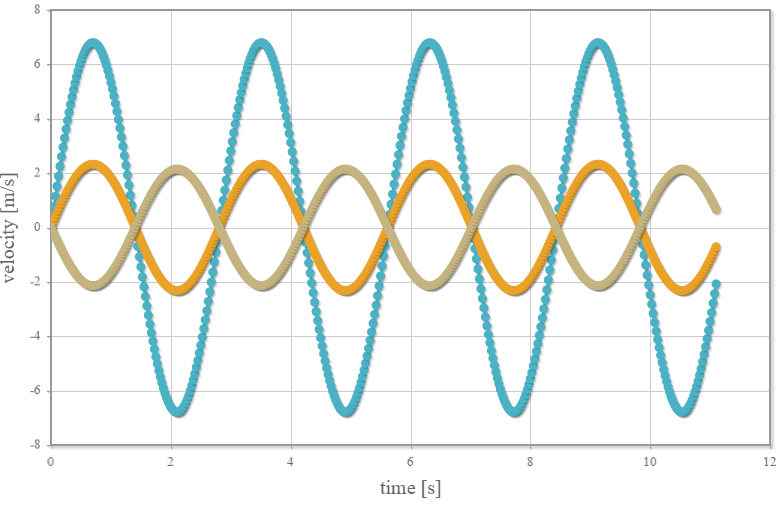
時刻vs速度のグラフ
時刻 $t$[s] の球体の速度を$v(t)$[m/s]と表した場合、時刻と速度の関係は $ v(t) = -L\omega \sin( \omega t ) $ となります。 なお、位置と速度は $v(t) = \frac{dz(t)}{dt}$ の関係があります。
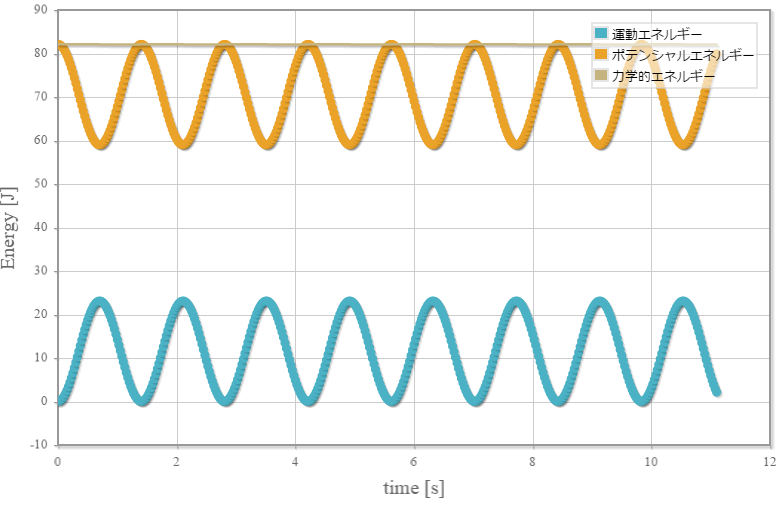
時刻vsエネルギーのグラフ
時刻 $t$[s] の運動エネルギーを$K(t)$、ポテンシャルを $U(t)$、力学的エネルギーを $E(t)$とした場合、それぞれの時間依存性は $K(t) = \frac{1}{2} m v(t)^2$、 $U(t) = \frac{1}{2} k x(t)^2 + mgz(t)$、$E(t) = K(t) + U(t)$ となります。 なお、この系では力学的エネルギーは保存するため、時間に対して一定値を取り続けます。