HOME > natural science Laboratory > コンピュータ・シミュレーション講座 > 仮想物理実験室

HTML5による有限要素法に基づいた2次元弾性体変形シミュレーション 第4回

文責：佐瀬 一弥 （2015年4月 1日） カテゴリ：仮想物理実験室(325)

第1回　メッシュのデータ構造とCanvas要素による描画
第2回　Numeric.jsによる線形代数
第3回　変形の表現と境界条件
第4回　全体剛性マトリクスの組み立てと剛性方程式の求解

第4回では全体剛性マトリクスの組み立てと剛性方程式の求解について説明します． 第3回で境界条件の設定を行いましたが，強制変位を与えていない節点の変位は未知のままでした． 今回の記事で扱う内容ですべての節点における未知数が計算できるようになります．

要素剛性マトリクス

三角形定ひずみ要素の場合， 要素剛性マトリクスは次式のように行列積で求められます．

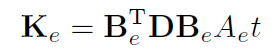
ここで，Ke は要素剛性マトリクス，Be はひずみ-変位マトリクス， D は弾性マトリクス，Ae は面積，tは厚さです．添え字の e は要素によって異なる（要素に依存する）ことを示します．

平面応力状態における二次元等方弾性体の場合，弾性マトリクスDは次式となります．

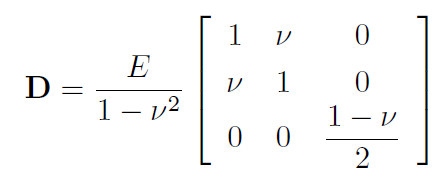
ここで，Eはヤング率，νはポアソン比です． つまり，D は材料の性質に関する行列であることがわかります． なお，本記事では材料が均質であることを仮定します． そのため，D に添え字 e をつけていません．

定ひずみ三角形要素の場合，ひずみ-変位マトリクスBeは次式となります．

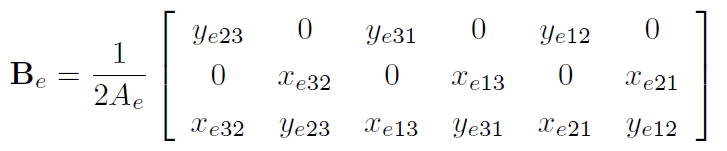
ここで，x_eij = x_ei - x_ej （x_ei, x_ej は頂点iまたは頂点jのx座標，i,j = 1, 2, 3) です。y_eijについても同様です．

面積 Ae は次のように求めることができます．

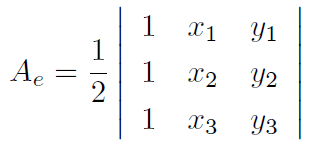
今回はマトリクス D, Be が何を意味するのかには触れませんが，今後の記事の中で必要に応じて説明したいと思います． 要素剛性マトリクスが上記の式によって求められることを認めるとして，実装について考えることにします． 以下の疑似コードを参照してください． これまでの記事で，メッシュの形状に関する情報はすでに用意してあるので， 新たな情報としてヤング率，ポアソン比，材料の厚さの材料特性に関する値が必要となります． 材料特性と節点の初期位置，三角形の節点番号リストがあれば要素剛性マトリクスが作成できます． JavaScriptによる実装は記事の最後にまとめて示しますので， 詳細な実装を確認したい方は最後のfem.js で定義されている FEM.assembleStiffnessMatrix メソッドを参照してください． 

        // 疑似コード
        // numElemetns: 三角形要素数
        // E:           ヤング率
        // nu:          ポアソン比
        // thickness:   厚さ
        // Ke:          要素剛性マトリクス (配列サイズ numElements x 6 x 6)
        // D:           弾性マトリクス (配列サイズ 3 x 3)
        // Ae:          三角形の面積
        // Be:          ひずみ-変位マトリクス (配列サイズ 3 x 6)
        // x0, y0:      頂点0のx座標およびy座標, x1,y1,x2,y2 についても同様
        // pos:         頂点座標配列
        // tri:         三角形を構成する節点番号リスト
        Ke = new Array(numElements);
       	D = calcD(E, nu);
        for(var e = 0; e < numElements; ++e){
        	x0 = pos[tri[e][0]][0];  y0 = pos[tri[e][0]][1];
        	x1 = pos[tri[e][1]][0];  y1 = pos[tri[e][1]][1];
        	x2 = pos[tri[e][2]][0];  y2 = pos[tri[e][2]][1];
            Ae = calcAe([x0,y0], [x1,y1], [x2,y2]);
            Be = calcBe([x0,y0], [x1,y1], [x2,y2]);
        	Ke[e] = Be.transpose() * D * Be * Ae * thickness;	
        }

※ 実際のコードでは行列演算を numeric.js で実装することになります．
※ calcD(), calcAe(), calcBe() は上記の式に従って定義する必要があります．
※ x0, y0... は数式と合わせるために追加した変数であり，実際にはこのように一時的に変数に格納する必要はありません．

全体剛性マトリクスの組み立て

要素剛性マトリクスを元に全体剛性マトリクスを組み立てます． 第１回で扱った下図に示す２つの三角形からなるメッシュを題材に説明します．

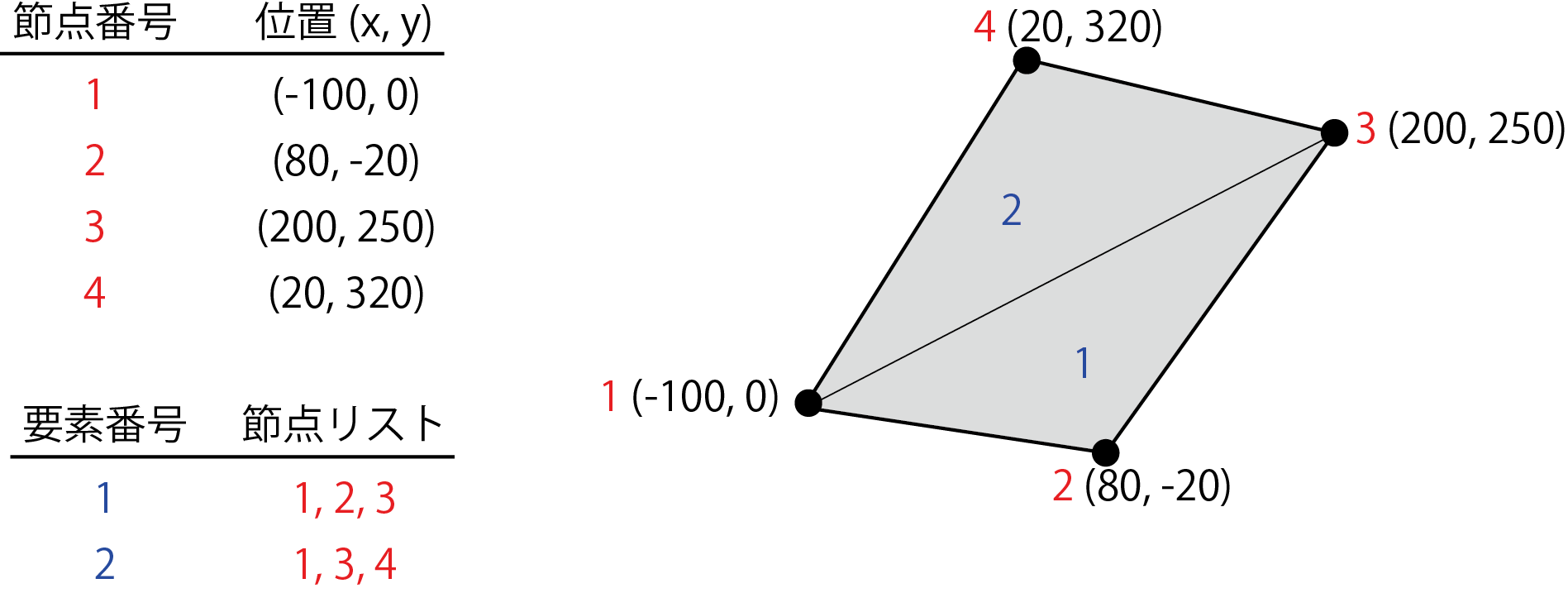
このメッシュの場合の全体剛性マトリクスは 下図のように要素剛性マトリクスを全体剛性マトリクスと同じ大きさに拡張して足すことで得られます． 図中のKについている上付き数字は要素番号，下付き数字は要素剛性マトリクスにおけるインデックスを表しています（次の図も参照）．

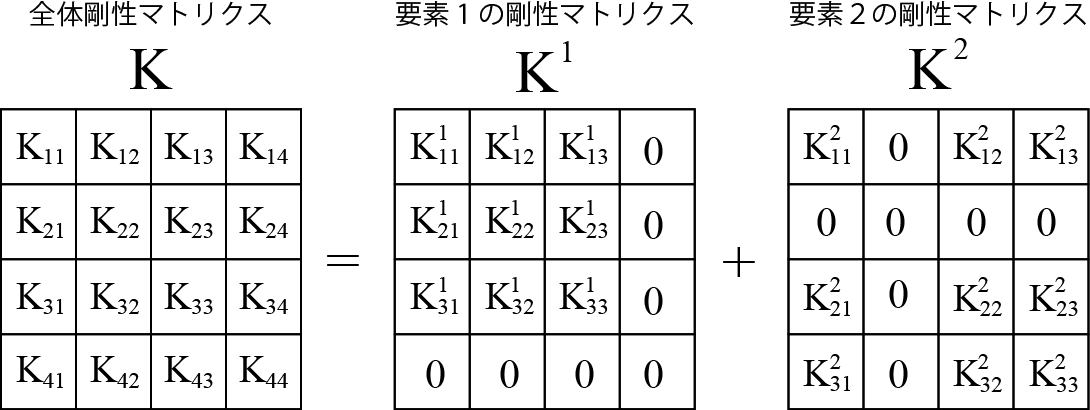
要素剛性マトリクスを拡張するには，要素を構成する節点番号リストを参照します．
下図のように，要素2の要素剛性マトリクスの2行3列にある部分行列は， 3行4列に移動しています． これは要素2の頂点2は全体メッシュでは3番, 頂点3は全体メッシュでは4番であるという関係に基づいています． すべての要素剛性マトリクスの部分行列についてこの処理を行うことで， 要素剛性マトリクスを拡張します．

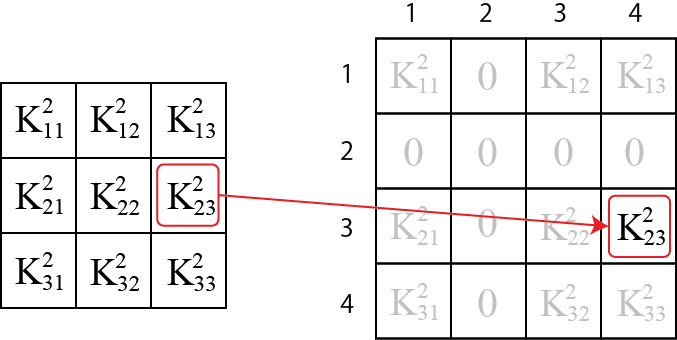
拡張したマトリクスは実際はメモリに格納しなおす必要はなく， 全体剛性マトリクスの該当箇所に順に足しこむことで目的が達成できます． 以下に疑似コードを示します．詳細な実装は記事の最後に示す fem.js の FEM.assembleStiffnessMatrix メソッドを参照してください． 

        // 疑似コード
        // K:        全体剛性マトリクス
        
        K = zeroMatrix(numNodes, numNodes);	// 零行列で初期化
        for(var e = 0; e < numElements; ++e){
            for(var i = 0; i < 3; ++i){
                for(var j = 0; j < 3; ++j){
                    K(tri[e][i], tri[e][j]) += Ke[e](i, j);		
                    // ↑注意: 疑似コード 
                    // K(a, b) はKを2×2ごとに分割したときの a行 b列 部分行列を表すものとして記述した
                }
            }
        }

上記コードは記述を平易にするため部分行列の足し算をそのまま記述していますが， これを展開すると以下のような深い多重ループとなります． 

        // 疑似コード
        
        K = zeroMatrix(numNodes, numNodes);	// 零行列で初期化
        for(var e = 0; e < numElements; ++e){
            for(var i = 0; i < 3; ++i){
                for(var j = 0; j < 3; ++j){
                	for(var k = 0; k < 2; ++k){
                    	for(var l = 0; l < 2; ++l){
		                    K[2*tri[e][i]+k][2*tri[e][j]+l] += Ke[e][2*i+k][2*j+l];
                        }
                    }
                }
            }
        }

剛性方程式の求解

　次に剛性方程式を与えらえた境界条件のもとで解く方法について述べます． 第３回で述べたように，節点の変位既知 or 外力既知の分類を行いました． これによって変位ベクトルと外力ベクトルがそれぞれ変位既知 or 外力既知の成分に分割されました． この分割に対して整合性が取れるように全体剛性マトリクスも並べ替えて下の図のようにする必要があります．

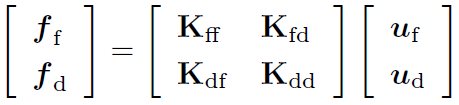
このように分割すると，uf, fd が未知数でその他は既知となります．まず，未知変数 uf は次の連立一次方程式を解くことで得られます．

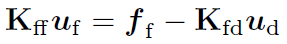
次に，得られた uf を用いて もうひとつの未知変数 fd を次の式により求められます．

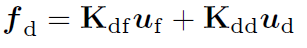
uf, fd が求められたら全体変位ベクトル，全体外力ベクトル，節点の現在位置を更新することができます．

さて，Kff, Kfd, Kdf, Kdd を作成するにはどうすればよいでしょうか． 第3回で uf, ud, ff, fd の作成のために用いた， dlist, flist という配列をここでも用います． Kff の作成のコードを以下示します． なお， Kff 作成コードとその下で示す Kfd 作成コードを比較する参考のために行をハイライトしました． 

        	for(var i = 0; i < flist.length; ++i){
            	for(var j = 0; j < flist.length; ++j){
                	for(var k = 0; k < 2; ++k){
                    	for(var l = 0; l < 2: ++l){
                        	Kff[2*i+k][2*j+l] = K[2*flist[i]+k][2*flist[j]+l];
                        }
                    }
                }
            }

Kfd は以下のように作成できます． 

        	for(var i = 0; i < flist.length; ++i){
            	for(var j = 0; j < dlist.length; ++j){
                	for(var k = 0; k < 2; ++k){
                    	for(var l = 0; l < 2: ++l){
                        	Kfd[2*i+k][2*j+l] = K[2*flist[i]+k][2*dlist[j]+l];
                        }
                    }
                }
            }

Kdf, Kdd も同様に作成することができますが， Kは対称行列となるため Kdf は Kfd の転置行列となり処理を省くことができます．

剛性方程式求解の結果の例

実装は次節に掲載しましたので，そちらを参考いただき，先に結果を示します．
main.js のメッシュ生成部と境界条件部を変更し，剛性方程式を解いた後に得られた 変形形状と等価節点外力を描画してみます．

	// 三角形メッシュ生成
	fem.generateTriangleMesh(200, 200, 2, 2);

	// 剛性マトリクスの組立
	fem.assembleStiffnessMatrix();
	 
	// 境界条件の設定
	fem.setBoundaryCondition(0, 200, [0, -40]);

↓

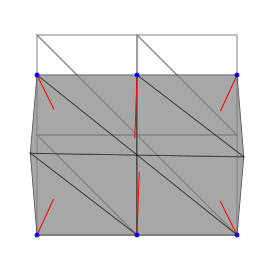
	// 三角形メッシュ生成
	fem.generateTriangleMesh(200, 200, 5, 5);

	// 剛性マトリクスの組立
	fem.assembleStiffnessMatrix();
	 
	// 境界条件の設定
	fem.setBoundaryCondition(0, 200, [0, -40]);

↓

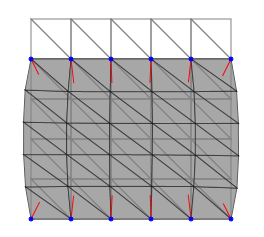
	// 三角形メッシュ生成
	fem.generateTriangleMesh(200, 200, 5, 5);

	// 剛性マトリクスの組立
	fem.assembleStiffnessMatrix();
	 
	// 境界条件の設定
	fem.setBoundaryCondition(0, 200, [20, 40]);

↓

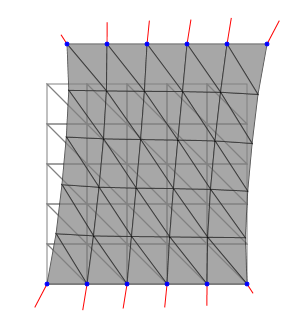
	// 三角形メッシュ生成
	fem.generateTriangleMesh(200, 200, 10, 10);

	// 剛性マトリクスの組立
	fem.assembleStiffnessMatrix();
	 
	// 境界条件の設定
	fem.setBoundaryCondition(0, 200, [20, 80]);

↓

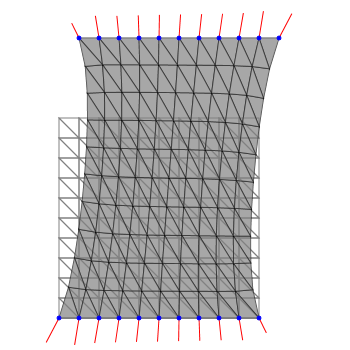
以上のように，板状の物体を引き延ばした様子が計算されました． 引き延ばすと板の中央部分がくびれる様子は妥当な挙動のように思われます． 等価節点外力も何となく妥当な分布を示しているように見えますが，これで良いのかどうかは判断が難しいですね． 一般的に正しい解析が行われているかどうかを判断するため， 数値解が偏微分方程式の厳密解と一致するかどうかを検証する必要があります． これについては今後の記事で説明する予定です．

JavaScriptによる実装

サンプルコード（zipファイル）

前回と同じように同一ディレクトリに index.html, main.js, fem.js, numeric-1.2.6.min.js を配置します． numeric-1.2.6.min.js は配布ページからダウンロードしたものを用いてください． fem.js, main.js, index.html の内容を以下に記します． 前回と変更のあった行をハイライトしていますので，今回の記事の前半部と照らし合わせてみてください．

fem.js

変更の概要は以下の通りです．
・FEMクラスのコンストラクタの引数として ヤング率，ポアソン比，厚さを渡すようにした．
・剛性マトリクス組み立てメソッド assembleStiffnessMatrix() を追加
・剛性方程式求解メソッド solve() を追加

// JavaScript source code
 
function FEM(youngModulus, poissonRatio, thickness) {
	this.pos     = [];				// 節点の初期位置
	this.initpos = [];				// 節点の現在位置
	this.tri     = [];				// 三角形要素の節点番号リスト
	this.u       = [];				// 全体変位ベクトル
	this.f       = [];				// 全体外力ベクトル
	this.dlist   = [];				// 変位既知節点リスト
	this.flist   = [];				// 外力既知節点リスト
	this.K       = [];				// 剛性マトリクス
	this.young   = youngModulus;	// ヤング率
	this.poisson = poissonRatio;	// ポアソン比
	this.thickness = thickness;		// 厚さ
}
 
// 三角形メッシュ生成メソッド
FEM.prototype.generateTriangleMesh = function (width, height, divx, divy) {
	// 節点の現在位置・初期位置の作成
	for(var i=0; i<divy+1; i++) {
		for(var j=0; j<divx+1; j++) {
			this.pos.push([width/divx*j-width*0.5, height/divy*i]);
			this.initpos.push([width/divx*j-width*0.5, height/divy*i]);
		}
	}
	// 三角形メッシュの作成
	for(var i=0; i<divy; i++) {
		for(var j=0; j<divx; j++) {
			this.tri.push([j+1+(divx+1)*i, j+1+(divx+1)*(i+1), j+(divx+1)*(i+1)]);
			this.tri.push([j+(divx+1)*i, j+1+(divx+1)*i, j+(divx+1)*(i+1)]);
		}
	}
	// 全体変位ベクトルの初期化
	this.u=numeric.rep([2*this.pos.length], 0);
}

// 剛性マトリクスの組み立て
FEM.prototype.assembleStiffnessMatrix = function(){

	this.K = numeric.rep([2*this.pos.length, 2*this.pos.length], 0);

	var D  = calcDmatrix(this.young, this.poisson);
	for(var e = 0; e < this.tri.length; ++e) {

		// calc elementa data
		var area = calcArea(
			this.pos[this.tri[e][0]], 
			this.pos[this.tri[e][1]], 
			this.pos[this.tri[e][2]]
			);
		var Be = calcBmatrix(
			this.pos[this.tri[e][0]], 
			this.pos[this.tri[e][1]], 
			this.pos[this.tri[e][2]],
			area
			);
		var Ke = numeric.dot(numeric.transpose(Be), D);	// Be.transpoes() * D
		Ke = numeric.dot(Ke, Be);						// Be.transpoes() * D * Be
		Ke = numeric.mul(Ke, area*this.thickness);		// Be.transpoes() * D * Be * Ae * t

		// assemble
		for(var i = 0; i < 3; ++i) {
			for(var j = 0; j < 3; ++j) {
				for(var k = 0; k < 2; ++k) {
					for(var l = 0; l < 2; ++l) {
						this.K[2*this.tri[e][i]+k][2*this.tri[e][j]+l] += Ke[2*i+k][2*j+l];
					}
				}
			}
		}
	}

	// 弾性マトリクス作成関数
	function calcDmatrix(young, poisson) {
		var D = numeric.rep([3,3], 0);
		D[0][0] = 1.0;
		D[0][1] = poisson;
		D[1][0] = poisson;
		D[1][1] = 1.0;
		D[2][2] = (1.0- poisson)/2.0;
		return numeric.mul(young/(1.0-poisson*poisson), D);
	}

	// 要素面積計算関数
	function calcArea(p1, p2, p3) {
		var mat = [
			[1, p1[0], p1[1]], 
			[1, p2[0], p2[1]], 
			[1, p3[0], p3[1]]
			];
		return numeric.det(mat)/2.0;
	}

	// ひずみ-変位マトリクス作成関数
	function calcBmatrix(p1, p2, p3, area) {
		var B = numeric.rep([3, 6], 0);
		B[0][0] = p2[1] - p3[1];
		B[0][2] = p3[1] - p1[1];
		B[0][4] = p1[1] - p2[1];
		B[1][1] = p3[0] - p2[0];
		B[1][3] = p1[0] - p3[0];
		B[1][5] = p2[0] - p1[0];
		B[2][0] = p3[0] - p2[0];
		B[2][1] = p2[1] - p3[1];
		B[2][2] = p1[0] - p3[0];
		B[2][3] = p3[1] - p1[1];
		B[2][4] = p2[0] - p1[0];
		B[2][5] = p1[1] - p2[1];
		return numeric.mul(1.0/(2.0*area), B);
	}
}



// 境界条件の設定
FEM.prototype.setBoundaryCondition = function (zfix, zdisp, disp) {
	 
	this.dlist = [];
	this.flist = [];
		 
	this.u = numeric.rep([2*this.pos.length], 0);
	this.f = numeric.rep([2*this.pos.length], 0);
	 
	// 底面のノードに強制変位を与える
	for(var i=0; i<this.pos.length; i++){
		if(this.initpos[i][1] === zfix){
			this.u[2*i]   = 0;
			this.u[2*i+1] = 0;
			this.dlist.push(i);
		}else if(this.initpos[i][1] === zdisp){
			this.u[2*i]   = disp[0];
			this.u[2*i+1] = disp[1];
			this.dlist.push(i);
		}else{
			this.f[2*i]   = 0;
			this.f[2*i+1] = 0;
			this.flist.push(i);
		}
	}
	 
}
 
// 剛性方程式の求解
FEM.prototype.solve = function (){
 
	// make ud
	var ud = [];
	for(var i=0; i<this.dlist.length; ++i){
		for(var j = 0; j < 2; ++j) {
			ud.push(this.u[2*this.dlist[i]+j]);
		}
	}

	// make ff
	var ff = [];
	for(var i=0; i<this.flist.length; ++i){
		for(var j = 0; j < 2; ++j) {
			ff.push(this.f[2*this.flist[i]+j]);
		}
	}

	// make Kff
	var Kff = numeric.rep([2*this.flist.length, 2*this.flist.length], 0);
	for(var i = 0; i < this.flist.length; ++i) {
		for(var j = 0; j < this.flist.length; ++j) {
			for(var k = 0; k < 2; ++k) {
				for(var l = 0; l < 2; ++l) {
					Kff[2*i+k][2*j+l] = this.K[2*this.flist[i]+k][2*this.flist[j]+l];
				}
			}
		}
	}

	// make Kfd
	var Kfd = numeric.rep([2*this.flist.length, 2*this.dlist.length], 0);
	for(var i = 0; i < this.flist.length; ++i) {
		for(var j = 0; j < this.dlist.length; ++j) {
			for(var k = 0; k < 2; ++k) {
				for(var l = 0; l < 2; ++l) {
					Kfd[2*i+k][2*j+l] = this.K[2*this.flist[i]+k][2*this.dlist[j]+l];
				}
			}
		}
	}

	// make Kdf
	var Kdf = numeric.transpose(Kfd);

	// make Kdd
	var Kdd = numeric.rep([2*this.dlist.length, 2*this.dlist.length], 0);
	for(var i = 0; i < this.dlist.length; ++i) {
		for(var j = 0; j < this.dlist.length; ++j) {
			for(var k = 0; k < 2; ++k) {
				for(var l = 0; l < 2; ++l) {
					Kdd[2*i+k][2*j+l] = this.K[2*this.dlist[i]+k][2*this.dlist[j]+l];
				}
			}
		}
	}

	// solve
	var b = numeric.clone(ff);					// ff
	b = numeric.sub(b, numeric.dot(Kfd, ud));	// ff - Kfd * ud
	var uf = numeric.solve(Kff, b);				// solve Kff * uf = ff - Kfd * ud

	// fd = Kdf * uf + Kdd * ud
	var fd = numeric.add(numeric.dot(Kdf, uf), numeric.dot(Kdd, ud));

	// update u
	for(var i = 0; i < this.flist.length; ++i) {
		for(var j = 0; j < 2; ++j) {
			this.u[2*this.flist[i]+j] = uf[2*i+j];
		}
	}

	// update f
	for(var i = 0; i < this.dlist.length; ++i) {
		for(var j = 0; j < 2; ++j) {
			this.f[2*this.dlist[i]+j] = fd[2*i+j];
		}
	}
	 
}

main.js

main.js は以下のように メソッド assembleStiffnessMatrix() と solve() の呼び出しと， 等価節点外力の描画を追加します． また，メッシュの描画の様子がわかりやすいように色・透明度・塗りなどを変更しました． 

// JavaScript source code
// HTMLを読み終わった後に実行する関数
$(document).ready(function () {
 
    // FEMクラスのインスタンス化
    var young     = 1e6;    // ヤング率
    var poisson   = 0.4;    // ポアソン比
    var thickness = 1.0;    // 厚さ
    var fem=new FEM(young, poisson, thickness);
     
    // 三角形メッシュ生成
    fem.generateTriangleMesh(200, 200, 5, 5);
     
    // 剛性マトリクスの組立
    fem.assembleStiffnessMatrix();
      
    // 境界条件の設定
    fem.setBoundaryCondition(0, 200, [20, 40]);

    // 剛性方程式の求解
    fem.solve();

    // 変位ベクトルによる現在形状の更新
    for(var i=0; i<fem.pos.length; i++) {
        for(var j=0; j<2; j++){
            fem.pos[i][j] = fem.initpos[i][j] + fem.u[2*i+j];
        }
    }
     
    // 2dコンテキスト取得
    var canvas  = $("#model_viewer");
    var context = canvas.get(0).getContext("2d");
    canvas.get(0).width  = canvas.get(0).clientWidth;
    canvas.get(0).height = canvas.get(0).clientHeight;
    var canvasWidth  = canvas.get(0).width;
    var canvasHeight = canvas.get(0).height;
 
    // 座標変換
    var xzero = canvasWidth*0.5; // キャンバス要素の幅の半分
    var yzero = canvasHeight*0.9; // キャンバス要素の高さの90%の部分
    context.setTransform(1, 0, 0, -1, xzero, yzero);
 
    // 初期形状の描画
    context.strokeStyle = 'gray';
    for(var i=0; i<fem.tri.length; i++) {
        drawtri(fem.initpos[fem.tri[i][0]], fem.initpos[fem.tri[i][1]], fem.initpos[fem.tri[i][2]]);
    }
 
    // 現在形状の描画
    context.strokeStyle = 'black';
    context.fillStyle   = 'gray';
    context.globalAlpha = 0.7;
    for(var i=0; i<fem.tri.length; i++) {
        drawtri(fem.pos[fem.tri[i][0]], fem.pos[fem.tri[i][1]], fem.pos[fem.tri[i][2]]);
        filltri(fem.pos[fem.tri[i][0]], fem.pos[fem.tri[i][1]], fem.pos[fem.tri[i][2]]);
    }
    context.globalAlpha = 1.0;

    // 等価節点外力の描画
    context.strokeStyle = 'red';
    for(var i=0; i<fem.pos.length; ++i) {
        var fScale = 3e-6;
        var fDist = numeric.add(fem.pos[i], [fScale*fem.f[2*i], fScale*fem.f[2*i+1]]);
        drawLine(fem.pos[i], fDist);
    }

    // 変位既知節点の描画
    context.strokeStyle = 'blue';
    context.fillStyle   = 'blue';
    for(var i=0; i<fem.dlist.length; i++) {
        drawCircle(fem.pos[fem.dlist[i]], 2);
    }
 
    // 線の描画関数
    function drawLine(p1, p2) {
        context.beginPath();
        context.moveTo(p1[0], p1[1]);
        context.lineTo(p2[0], p2[1]);
        context.stroke();
    }
    // 円の描画関数
    function drawCircle(p, radius) {
        context.beginPath();
        context.arc(p[0], p[1], radius, 0, 2*Math.PI, true);
        context.stroke();
        context.fill();
    }
    // 三角形の描画関数
    function drawtri(p1, p2, p3) {
        context.beginPath();
        context.moveTo(p1[0], p1[1]);
        context.lineTo(p2[0], p2[1]);
        context.lineTo(p3[0], p3[1]);
        context.closePath();
        context.stroke();
    }
    // 三角形の描画関数
    function filltri(p1, p2, p3) {
        context.beginPath();
        context.moveTo(p1[0], p1[1]);
        context.lineTo(p2[0], p2[1]);
        context.lineTo(p3[0], p3[1]);
        context.closePath();
        context.fill();
    }
});

index.html

index.htmlは変更がありませんが，再掲します． 

<!doctype html>
<html>
<head>
            <meta charset=\"utf-8\">
            <title>FEM</title>
            <!-- スタイルシート -->
            <style type=\"text/css\">
                #model_viewer {
                    width: 500px;
                    height: 500px;
                    border: 1px solid #000000;
                    background-color: #FFFFFF;
                }
            </style>
            <!--  jquery -->
            <script type=\"text/javascript\" src=\"http://ajax.googleapis.com/ajax/libs/jquery/1/jquery.min.js\"></script>
            <!--  numeric javascript -->
            <script type=\"text/javascript\" src=\"numeric-1.2.6.min.js\"></script>
            <!-- 自分のjavascriptコード -->
            <script type=\"text/javascript\" src=\"fem.js\"></script>
            <script type=\"text/javascript\" src=\"main.js\"></script>
</head>
<body>
            <canvas id=\"model_viewer\"></canvas>
</body>
</html>

第1回　メッシュのデータ構造とCanvas要素による描画
第2回　Numeric.jsによる線形代数
第3回　変形の表現と境界条件
第4回　全体剛性マトリクスの組み立てと剛性方程式の求解



タグ：

▲このページのトップ ｜ NPO法人 natural science トップ

関連記事

仮想物理実験室

【第８話】有限の高さの障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.29 【遠藤 理平｜仮想物理実験室】

【第７話】無限に高い障壁に向けた電子パルスの照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.24 【遠藤 理平｜仮想物理実験室】


【第６話】無限に高い障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.23 【遠藤 理平｜仮想物理実験室】

【第５話】電子パルスの運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.21 【遠藤 理平｜仮想物理実験室】


【第４話】電子パルスの作り方【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.20 【遠藤 理平｜仮想物理実験室】

【第３話】自由粒子の運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.19 【遠藤 理平｜仮想物理実験室】


【第２話】自由粒子のスナップショット【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.18 【遠藤 理平｜仮想物理実験室】

【第１話】プログラムの動作確認【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.17 【遠藤 理平｜仮想物理実験室】


１０日で作る量子ドットコンピュータ～動作原理を数値シミュレーション！～【５日目】１量子ビット万能量子ゲートを設計しよう！ 2019.09.06 【遠藤 理平｜仮想物理実験室】

１０日で作る量子ドットコンピュータ～動作原理を数値シミュレーション！～【４日目】量子井戸の電子状態の基礎実験３：２重量子井戸で量子ビットを改良！ 2019.08.27 【遠藤 理平｜仮想物理実験室】



▲このページのトップ ｜ NPO法人 natural science トップ




Warning: mysqli_connect(): (28000/1045): Access denied for user 'xsvx1015071_ri'@'sv102.xserver.jp' (using password: YES) in /home/xsvx1015071/include/natural-science/include_counter-d.php on line 8
MySQL DBとの接続に失敗しました