古典ルンゲ・クッタ法によるニュートンの運動方程式の数値計算

局所計算精度が４次である古典ルンゲ・クッタ法を用いて、２階常微分方程式であるニュートンの運動方程式を解いて、所定の精度が得られていることを確認します。 質量m、バネ定数kの調和振動子（単振動）に対するニュートン運動方程式から得られる位置に対する方程式は次のとおりです。

ルンゲ・クッタ法は１階の微分方程式で成り立つ公式なので、上記の２階微分方程式を２つの１階微分方程式に分解して、連立微分方程式の形にします。

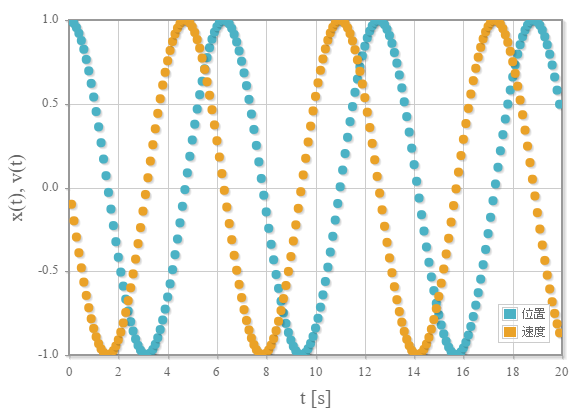
連立微分方程式と言っても、実質的には独立しているので簡単にルンゲ・クッタ法に適用することができます。 次のグラフはの範囲で、 上記調和振動子の時間発展の計算結果（位置と速度）と、計算誤差（解析解との差）の分割数依存性です。

調和振動子（単振動）の時間発展

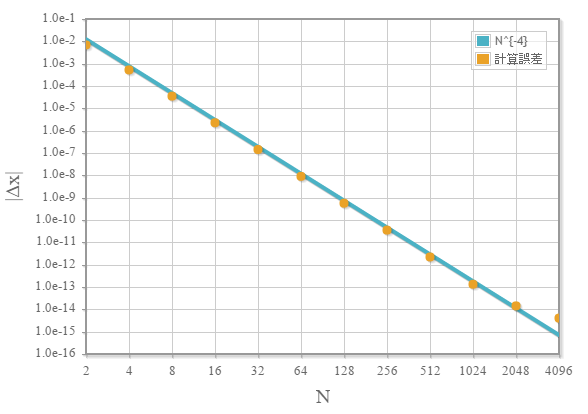
計算誤差の分割数依存性

分割数Nの場合、時間間隔をとして計算しています。 分割数に対して、計算誤差は４次となることが確認できます。

計算アルゴリズム（古典ルンゲ・クッタ法）

//計算パラメータ
var k = 1;  //バネ定数
var m = 1;  //質量
var T = 20; //終了時間

//質点に加わる力
function F( t, x, v ){
	return -k　/　m * x;
}
//dx/dt = v;
function V( t, x, v ){
	return v;
}
//ルンゲクッタ法による次ステップの計算
function RK4 ( F, V, dt, t, x, v ){
	var k1_x = V( t,        x,             v );
	var k1_v = F( t,        x,             v );
	var k2_x = V( t + dt/2, x + k1_x*dt/2, v + k1_v*dt/2 );
	var k2_v = F( t + dt/2, x + k1_x*dt/2, v + k1_v*dt/2 );
	var k3_x = V( t + dt/2, x + k2_x*dt/2, v + k2_v*dt/2 );
	var k3_v = F( t + dt/2, x + k2_x*dt/2, v + k2_v*dt/2 );
	var k4_x = V( t + dt  , x + k3_x*dt,   v + k3_v*dt   );
	var k4_v = F( t + dt  , x + k3_x*dt,   v + k3_v*dt   );
	return { 
		x : dt / 6 *(  k1_x + 2*k2_x + 2*k3_x + k4_x ),
		v : dt / 6 *(  k1_v + 2*k2_v + 2*k3_v + k4_v )
	};
}