高速フーリエ変換のテスト（係数の定義範囲の変更）

「高速フーリエ変換のテスト（矩形関数）」では、 の範囲の整数で定義しましたが、 対象とする系によってはの範囲で定義するほうが理解しやすいこともあります。 そこで、nの正負の関係を調べるために 前項で示した展開係数のnに-nを代入すると >

という結果になります。「*」は複素共役を表す記号です。つまり、展開係数の実部と虚部は

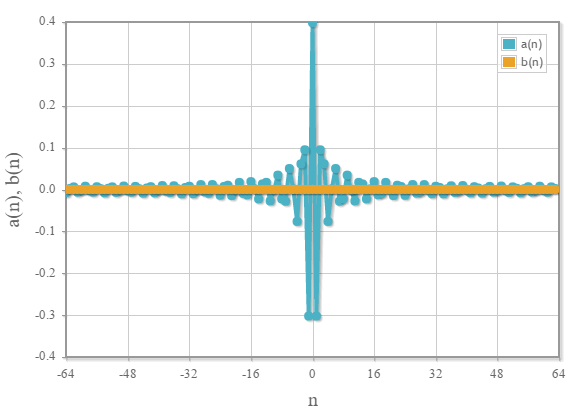
という関係があるわけです。 このことから前項の高速フーリエ変換の結果から、展開係数の範囲を に直接変換することができます。 次のグラフは前項と同じ矩形関数のフーリへ変換の結果を変換した結果です。

//フーリへ変換の実行
FFT( an, bn, N );

//-N/2 から N/2-1 の展開係数を格納する配列（an_, bn_）	
for( var n = 0; n < N; n++ ){
	var nn;

	if( n < N/2 ) nn = N/2 + n;
	else nn = n - N/2; 

	an_[ n ] = an[ nn ];
	bn_[ n ] = bn[ nn ];
}

展開係数

※実物は画像をクリックするとご覧いただけます。

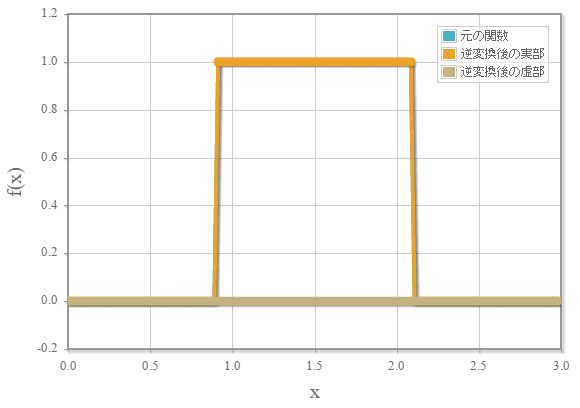
逆フーリエ変換

で定義された展開係数を に変換後、逆フーリエ変換を実行した結果です 意図通り結果が得られていることが確認できました。

※実物は画像をクリックするとご覧いただけます。

//-N/2 から N/2-1 の展開係数を格納する配列（an_, bn_）	から元の範囲の展開係数へ変換
for( var n = 0; n < N; n++ ){

	var nn;
	if( n < N/2 ) nn = N/2 + n;
	else nn = n-N/2; 

	_an[ n ] = an_[ nn ];
	_bn[ n ] = bn_[ nn ];

}
//逆フーリエ変換の実行
FFT( _an, _bn, N, true);