2次元高速フーリエ変換のテスト(矩形関数)
の範囲で定義される2変数実関数
を正規直交系を成す三角関数の和で表される指数関数を用いて、次の通りに展開することを考えます。
展開係数は一般的に複素数です。
展開係数
は指数関数の完全性から、元の関数から一意に
と与えられます。これはフーリエ級数展開と呼ばれ、もとの関数が空間分布であれば波数成分が、時間分布であれば周波数成分を取得することができます。 この2次元の展開係数の計算は「高速フーリエ変換のテスト(矩形関数)」で示した1次元FFTを2段階で適用することで行うことができます。上記の式を次のとおり変形します。
このように変更することで、上記のを1次元FFTで計算することができ、さらにその結果も1次元FFTで計算することができます。
高速フーリエ変換の例:矩形関数
の範囲で定義される実関数の例として矩形関数
かつ
上記以外
の展開係数を高速フーリエ変換を用いて計算します。は矩形の幅を表します。
以下の結果はN=128の場合(2のべきである必要があります)です。
展開係数
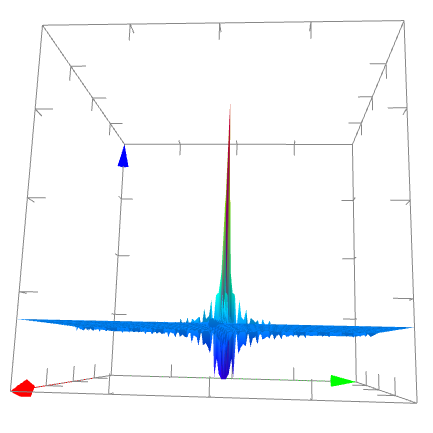
※実物は画像をクリックするとご覧いただけます。
逆フーリエ変換
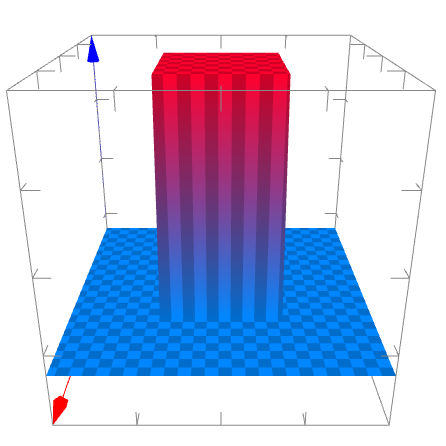
※実物は画像をクリックするとご覧いただけます。
上記で計算した展開係数を用いて逆フーリエ変換を行って元の関数を再現した結果です。元の矩形関数をほぼ再現していることがわかります。
計算方法
「高速フーリエ変換のテスト(矩形関数)」で示したFFT関数を用いて2次元FFTの計算を行います。 「xan[ i ][ j ]」に元の関数の2次元格子状の値を与えます。2段階のFFT実行の結果に「yan[ i ][ j ]」と「ybn[ i ][ j ]」に展開係数が格納されます。
//展開係数の計算
function calculateCoefficients(){
for( var i=0; i<N; i++ ){
for( var j=0; j<N; j++ ){
var x = L/N * (i - N/2);
var y = L/N * (j - N/2);
xan[ i ][ j ] = f( x, y ); //元実関数
xbn[ i ][ j ] = 0;
}
}
for( var i=0; i<N; i++ ){
//x軸に平行なFFTの実行
FFT( xan[ i ], xbn[ i ], N );
}
for( var i=0; i<N; i++ ){
for( var j=0; j<N; j++ ){
yan[ i ][ j ] = xan[ j ][ i ];
ybn[ i ][ j ] = xbn[ j ][ i ];
}
}
for( var i=0; i<N; i++ ){
//y軸に平行なFFTの実行
FFT( yan[ i ], ybn[ i ], N);
}
//yan[ i ][ j ] 、ybn[ i ][ j ]に結果が格納
}
反対に「yan[ i ][ j ]」と「ybn[ i ][ j ]」の展開係数から実空間の値の計算方法を次のとおりです。 2段階のFFTの結果「_yan[ i ][ j ]」、「_ybn[ i ][ j ] 」に結果が格納されます。
//逆変換の計算
function calculateInverse(){
for( var i=0; i<N; i++ ){
for( var j=0; j<N; j++ ){
_xan[ i ][ j ] = yan[ i ][ j ];
_xbn[ i ][ j ] = ybn[ i ][ j ];
}
}
for( var i=0; i<N; i++ ){
//kxに平行なFFTの実行
FFT( _xan[ i ], _xbn[ i ], N, true );
}
for( var i=0; i<N; i++ ){
for( var j=0; j<N; j++ ){
_yan[ i ][ j ] = _xan[ j ][ i ];
_ybn[ i ][ j ] = _xbn[ j ][ i ];
}
}
for( var i=0; i<N; i++ ){
//ky軸に平行なFFTの実行
FFT( _yan[ i ], _ybn[ i ], N, true);
}
//_yan[ i ][ j ]、_ybn[ i ][ j ] に結果が格納
}








































