シンプソンの積分公式(4次精度)による数値積分テスト
数値積分の計算精度が刻み幅の4次であるシンプソンの積分公式を用いて、与えられた1変数関数の積分値を計算して誤差を調べます。
具体的にはに対して
の範囲で積分した結果を解析解と比較します。
局所計算精度が4次なので1区間の計算誤差(局所誤差)は5次です。そのため積分区間全体における計算誤差(大局誤差)は4次となります。
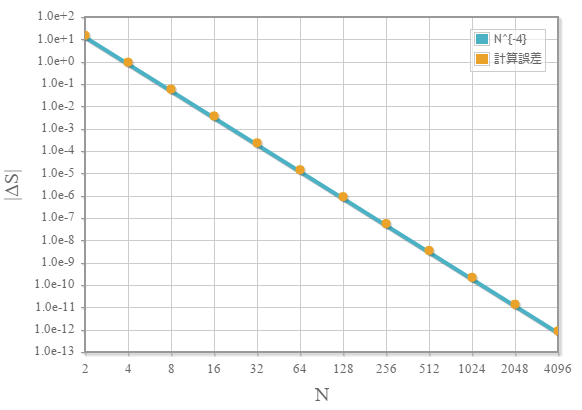
次のグラフは積分区間の分割数に対する計算誤差をプロットした結果です。大局計算誤差が4次であることが確認できます。
計算誤差
計算アルゴリズム(シンプソンの積分公式)
function SimpsonIntegral( f, min, max, N ){
//刻み幅
var delta = (max - min)/ N;
//和の値
var sum = 0;
for (var n = 1; n <= N/2; n++) {
//x_nの値
var x = min + delta * ( 2 * n - 1 );
sum += ( f(x - delta) + 4 * f(x) + f(x + delta)) / 3 ;
}
//積分値
return sum * delta;
}
物理シミュレーションについては「HTML5による物理シミュレーション」を参照ください。 数式の表示は「Tex表記によるHTML文書への式の埋め込み」をご覧ください。