ゼロから作るDeep Learning
準備３：多変数関数の数値微分と極小値の探索

昨今注目を集めているAI（人工知能）を学びたいと思い立ち、ディープラーニング（Deep Learning、深層学習）と呼ばれるAIの数理モデルである多層構造のニューラルネットワークを書籍「ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装」を参考にを独習していきたいと思います。本書籍ではプログラミング言語としてPythonが利用されていますが、本項ではJavaScriptで実装していきます。

目次

• 準備１：行列の和と積を計算する関数の実装
• 準備２：ベクトルと行列の積を計算する関数の実装
• 準備３：多変数関数の数値微分と極小値の探索
• １．１層ニューラルネットワークの実装（バイアスなし、活性化関数なし、学習なし）
• ２．１層ニューラルネットワークへのバイアスと活性化関数の追加
• ３．1n1型２層ニューラルネットワークの実装（学習なし）
• ４．１変数関数を学習させてみる１：勾配法による学習計算アルゴリズム
• ５．１変数関数を学習させてみる２：勾配法による学習計算アルゴリズムの実装
• ６．１変数関数を学習させてみる３：ニューロン数による学習効果の違い
• ７．誤差逆伝搬法（バックプロパゲーション）の導出
• ８．順伝播型ニューラルネットワーク「FFNNクラス」の実装（JavaScript）
• ９．三角関数のサンプリング学習（WebWorkersによる並列計算）
• 10．学習後の各層ニューロンの重みの可視化
• 11．層数とニューロン数による学習効果の違い

Deep Learning では、損失関数と呼ばれる正解からのズレを最小化することを学習と位置づけています。 損失関数はパラメータの数分の引数をもつ多変数関数で定義され、入力に対して多変数関数が小さくなるようにパラメータを調整します。 その際に必要となるのが多変数関数の数値微分です。本項では次の２変数関数の数値微分の計算方法と最小値を探索する計算アルゴリズムについて解説します。

多変数関数の数値微分

多変数関数の数値微分の題材として次の２変数関数を取り上げます。

多変数関数の数値微分の定義

多変数関数の微分の定義は次のとおりです。

上記の関数のように関数形があらかじめ分かっている場合には微分を解析的に計算することができますが、関数形が未知の場合には数値的に計算するしかありません。 コンピュータでは無限小を扱うことができないため、微分をdを小さな値として次のとおりに定義します。

これで(x,y)地点における勾配を得ることができます。原理的にはdは小さいほど真の値に近づくはずですが、コンピュータが扱うことのできる有効桁数が倍精度で１５桁程度なので、小さすぎると桁落ちのために精度が反対に悪化します。 ニューラルネットワークでは正確な勾配は必要ないので探索する領域の1/1000程度で十分たと思います。ただし、上記のアルゴリズムは(x,y)地点の勾配を(x,y)と(x+d,y)と(x,y+d)の地点の値を用いていて対称性が悪いです。 次のように定義を変更することで対称性を良くなり、計算精度がdの１次分だけ上がります。

先の計算アルゴリズムは前進差分による数値微分、後は中心差分による数値微分と呼ばれます。

勾配法による極小値の探索

勾配を計算することができると、任意の地点から出発して勾配の下向きに向かって移動することで極小値にたどり着くことができます。 具体的には初期値からスタートして次の計算アルゴリズムに従って計算します。

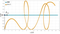
上記の計算アルゴリズムを用いて極小値の探索を実行してみましょう。極小値からのズレを

で評価した結果が次のグラフです。

２つのグラフは前進差分と中心差分における結果です。中心差分の方が極小値の真の値へ向うことが確認できました。