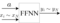ゼロから作るDeep Learning
1n1型２層ニューラルネットワークで１変数関数を学習させてみる３：ニューロン数による学習効果の違い

昨今注目を集めているAI（人工知能）を学びたいと思い立ち、ディープラーニング（Deep Learning、深層学習）と呼ばれるAIの数理モデルである多層構造のニューラルネットワークを書籍「ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装」を参考にを独習していきたいと思います。本書籍ではプログラミング言語としてPythonが利用されていますが、本項ではJavaScriptで実装していきます。

目次

• 準備１：行列の和と積を計算する関数の実装
• 準備２：ベクトルと行列の積を計算する関数の実装
• 準備３：多変数関数の数値微分と極小値の探索
• １．１層ニューラルネットワークの実装（バイアスなし、活性化関数なし、学習なし）
• ２．１層ニューラルネットワークへのバイアスと活性化関数の追加
• ３．1n1型２層ニューラルネットワークの実装（学習なし）
• ４．１変数関数を学習させてみる１：勾配法による学習計算アルゴリズム
• ５．１変数関数を学習させてみる２：勾配法による学習計算アルゴリズムの実装
• ６．１変数関数を学習させてみる３：ニューロン数による学習効果の違い
• ７．誤差逆伝搬法（バックプロパゲーション）の導出
• ８．順伝播型ニューラルネットワーク「FFNNクラス」の実装（JavaScript）
• ９．三角関数のサンプリング学習（WebWorkersによる並列計算）
• 10．学習後の各層ニューロンの重みの可視化
• 11．層数とニューロン数による学習効果の違い

ニューロン数による学習効果の違い

入力と出力が１個、隠れ層が１０個のニューロンで構成されるニューラルネットワークで学習した前項の３次関数の学習を題材にして、ニューロン数を変更した場合の学習効果の違いを検証します。

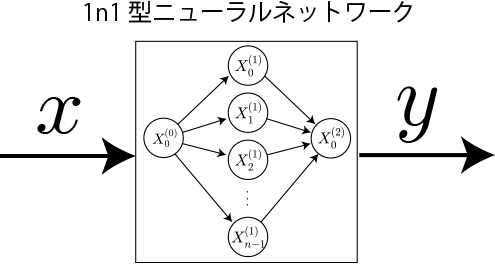
横軸：ニューロン数、縦軸：損失関数

次のグラフはニューロン数に対する損失関数の値（１０回の平均値）です。３本のグラフは学習回数1000回、2000回、3000回に対応します。 （※）読み込みごとに計算しているためグラフ表示までに１０秒程度掛かります。

実行ごとに若干のばらつきはありますが、ニューロン数は多い方、学習回数は多い方が損失関数の値が小さくなり、うまく学習できていることがわかります。 ３次関数の場合には、ニューロン数７個で2000回程度で概ね表現できていることがわかりました。今回は隠れ層が１層でしたが層数の依存性も今後検証していきます。