ゼロから作るDeep Learning
学習後の各層ニューロンの重みの可視化

昨今注目を集めているAI（人工知能）を学びたいと思い立ち、ディープラーニング（Deep Learning、深層学習）と呼ばれるAIの数理モデルである多層構造のニューラルネットワークを書籍「ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装」を参考にを独習していきたいと思います。本書籍ではプログラミング言語としてPythonが利用されていますが、本項ではJavaScriptで実装していきます。

目次

• 準備１：行列の和と積を計算する関数の実装
• 準備２：ベクトルと行列の積を計算する関数の実装
• 準備３：多変数関数の数値微分と極小値の探索
• １．１層ニューラルネットワークの実装（バイアスなし、活性化関数なし、学習なし）
• ２．１層ニューラルネットワークへのバイアスと活性化関数の追加
• ３．1n1型２層ニューラルネットワークの実装（学習なし）
• ４．１変数関数を学習させてみる１：勾配法による学習計算アルゴリズム
• ５．１変数関数を学習させてみる２：勾配法による学習計算アルゴリズムの実装
• ６．１変数関数を学習させてみる３：ニューロン数による学習効果の違い
• ７．誤差逆伝搬法（バックプロパゲーション）の導出
• ８．順伝播型ニューラルネットワーク「FFNNクラス」の実装（JavaScript）
• ９．三角関数のサンプリング学習（WebWorkersによる並列計算）
• 10．学習後の各層ニューロンの重みの可視化
• 11．層数とニューロン数による学習効果の違い

学習後の各層ニューロンの重みの可視化

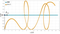
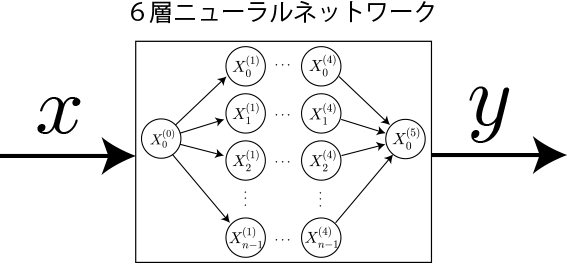
前項では６層ニューラルネットワーク（各層のニューロン数：1,10,10,10,10,1）で三角関数を学習させました。 およそ２万回の学習で関数の概形を表現できることを確認しました。本項では、学習後の各層ニューロンの重みがどのような値になったかを確認します。

実行結果

学習完了後に、各層のニューロン（1,10,10,10,10,1）をつなぐ重みの大きさをグラフ化します。横軸は１本のグラフはあるニューロンから次の層の各ニューロンへの重みを表します。 結論から言うと、学習後、三角関数をほとんど同様に表現できているものでも、重みを比較すると全く異なることがわかりました。つまり、一つの関数を表現するのに複数の状態が存在することを意味します。

【メモ】今回は実行時間を考慮して学習回数の区切りを1000回としています。（実行ごとに結果が異なり、学習がうまく行っていない場合が存在します。）