ゼロから作るDeep Learning
ニューラルネットワークでフーリエ変換を学習させてみよう１

昨今注目を集めているAI（人工知能）を学びたいと思い立ち、ディープラーニング（Deep Learning、深層学習）と呼ばれるAIの数理モデルである多層構造のニューラルネットワークを書籍「ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装」を参考にを独習していきたいと思います。本書籍ではプログラミング言語としてPythonが利用されていますが、本項ではJavaScriptで実装していきます。

目次

• 準備１：行列の和と積を計算する関数の実装
• 準備２：ベクトルと行列の積を計算する関数の実装
• 準備３：多変数関数の数値微分と極小値の探索
• １．１層ニューラルネットワークの実装（バイアスなし、活性化関数なし、学習なし）
• ２．１層ニューラルネットワークへのバイアスと活性化関数の追加
• ３．1n1型２層ニューラルネットワークの実装（学習なし）
• ４．１変数関数を学習させてみる１：勾配法による学習計算アルゴリズム
• ５．１変数関数を学習させてみる２：勾配法による学習計算アルゴリズムの実装
• ６．１変数関数を学習させてみる３：ニューロン数による学習効果の違い
• ７．誤差逆伝搬法（バックプロパゲーション）の導出
• ８．順伝播型ニューラルネットワーク「FFNNクラス」の実装（JavaScript）
• ９．三角関数のサンプリング学習（WebWorkersによる並列計算）
• 10．学習後の各層ニューロンの重みの可視化
• 11．層数とニューロン数による学習効果の違い

ニューラルネットワークでフーリエ変換を学習させてみよう１

これまではニューラルネットワークの練習がてら、あらかじめ与えた１変数関数を学習させました。 本項はx=0からx=1を100分割して、それぞれの地点における値を入力値として与えて、そのフーリエ級数展開の展開係数を出力値とするニューラルネットワークを構成することを考えます。 まずは動作確認として、２つの展開係数で展開される場合について実装します。

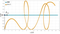
実行結果

下のグラフは、元の関数と入力値に対して出力した展開係数（）を用いて計算した結果です。 元の関数と概ね一致していることがわかります。