【ニューラルネットワークの基礎研究12】
学習効果を高めるにはディープ（層数）と並列数（ユニット数）のどちらが有効か？

ニューラルネットワークを勉強した後に、実際の系を学習させる際に問題になるのがネットワークの構造です。 特に中間層のユニット数や中間層の層数をどのように与えるかは自明ではなく、試行錯誤するしかありません。 これまで本シリーズでは初等関数を様々なネットワーク構造で学習させてみましたが、これまでの結果を踏まえて 「ネットワークに同じ自由度を与えるならば、中間層１層のユニット数を増やすべきか、中間層の層数を増やすべきか」という問いに一つの答えを出します。

【これまでの結果】
→ １変数の２次関数の学習 １ ２ ３ ４
→ 係数が変化する２次関数の学習 １ ２ ３ ４
→ べきが変化するべき関数の学習 １ ２ ３

対象とする関数

今回は「べきが変化する関数」を対象に比較を行います（指数が0から3まで変化）。

比較対象のネットワークの構造

本稿では中間層１層と中間層が４層で中間層ユニット数をそれぞれの10000個と100個とします。
このユニット数の場合、自由度（重みとバイアスの総数）が近いためです。

中間層１層（ユニット数10000個）

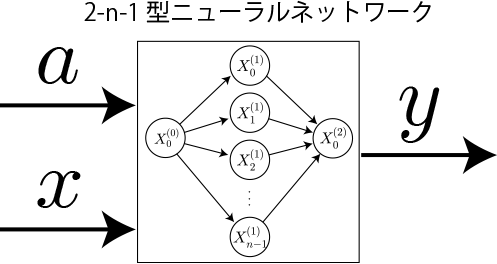
[重みの総数] = 2n + n = 3n
[バイアスの総数] = n
[合計] = 4n → 40000（n=10000）

中間層５層（ユニット数100個）

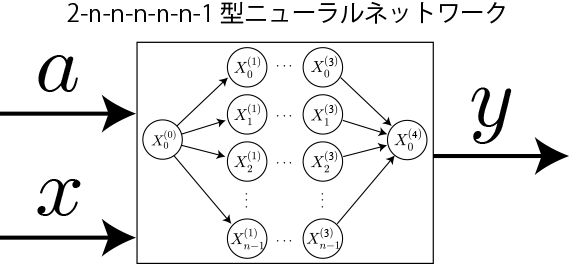
[重みの総数] = 2n + 4n^2 + n = 3n + 4n^2
[バイアスの総数] = 5n
[合計] = 8n + 4n^2 → 40800（n=100）

ニューラルネットワークの基本パラメータ

・ニューラルネットワークの構造：順伝播型ニューラルネットワーク（FFNN）
・学習方法：通常の勾配法（学習率固定、逆誤差伝搬法）
・学習率：eta = 0.01;
・ミニバッチ数：100 （サンプルは無限に用意できるためミニバッチという概念は存在しませんが、ランダムに用意したミニバッチ数分のサンプルに対する平均を用いて学習を進める）
・活性化関数（中間層）：ReLU（ランプ関数）
・活性化関数（出力層）：恒等関数
・損失関数：２乗和
※独立したネットワークを１０個用意してそれぞれ個別に学習させて、学習効果の高かった上位５つの「学習回数」vs「損失値」をグラフ化します。
※参考ページ

学習回数に対する損失値の比較

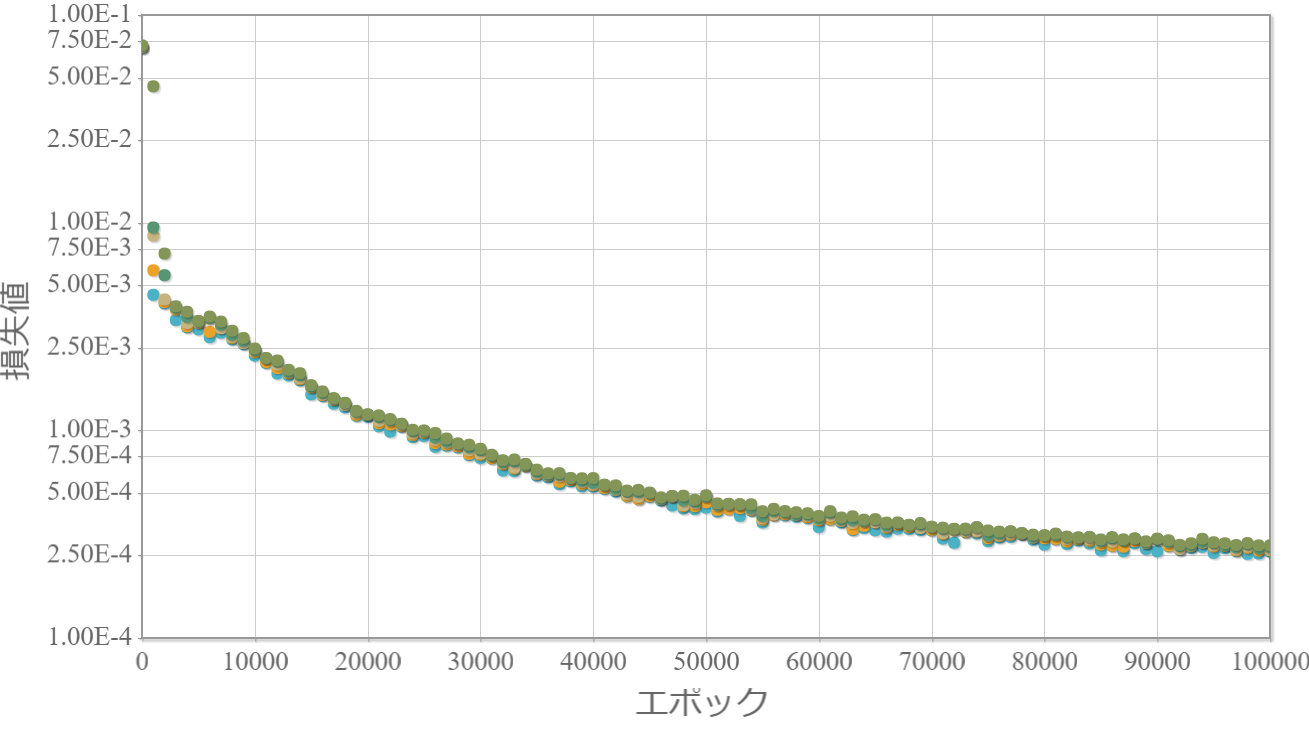
2-10000-1（１層）

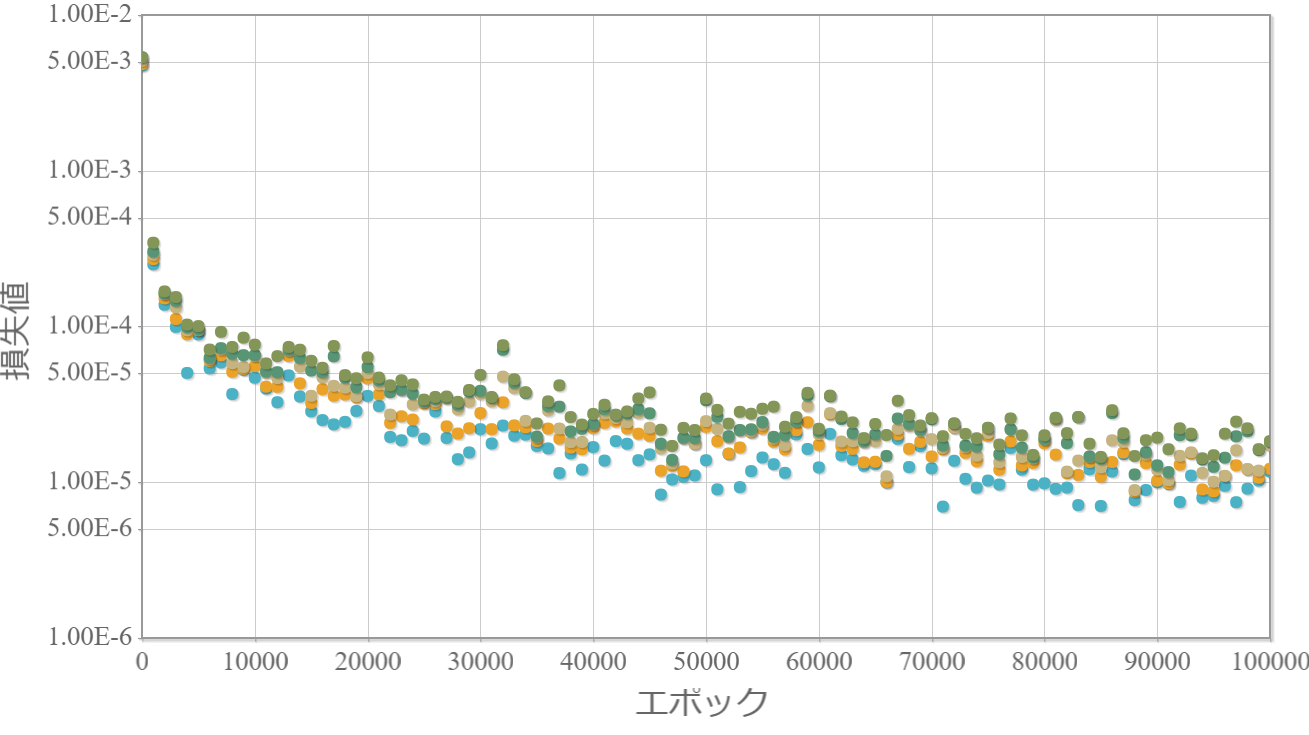
2-100-100-100-100-100-1（５層）

結果と考察

・５層の方が学習の安定性に欠けるが１層よりも損失値が1/20程度となった（学習回数100,000回）。
→ 学習効果は自由度（重みとバイアスの層数）だけでは決まらない。
→ 無論、ネットワークの構造が重要であることが確認できた。
・１層は安定しているのでまだ伸びしろがある（学習回数100,000回では足りない）。
→ 学習率を変化させる学習法を採用することで効果的に学習が進むと考えられる。
・１層の最終的な損失値（2.5E-4）は５層でわずか2000回で到達している。
→ 僅かな学習回数で学習成果が上がる多層化は概要を掴むのに適している。

今後の課題

・学習方法ごとの収束の違いを確かめる。

プログラムソース（C++）

・http://www.natural-science.or.jp/files/NN/FFNNs_epoch_Functions2.zip
※VisualStudio2017のソルーションファイルです。GCC（MinGW）でも動作確認しています。