【量子力学再入門1】
自由空間の量子粒子の運動
量子力学とは原子や電子といったナノスケールにおける粒子の運動を記述する物理学の一分野です。 メートルスケールで成り立つ「ニュートンの運動方程式」に対して、量子力学では「シュレディンガー方程式」と呼ばれる基礎方程式が成り立つと考えられています。本項では量子力学の基本的な問題を数値的に解くことで、量子力学の理解を深めることが目的とします。第一のテーマとして、下の図のような量子粒子の衝突をシミュレーションします。
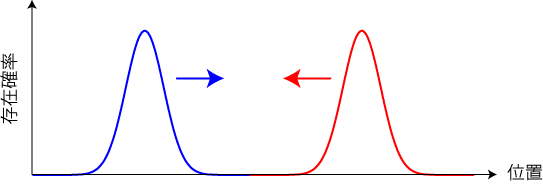
量子力学における粒子(量子粒子)は確率振幅と呼ばれる波で表されます。また、量子粒子は同じ種類の粒子の場合には衝突の前後で粒子の見分けがつかないという特徴があります。 まずはこの量子粒子の衝突の前に、粒子が1個の場合の運動をシミュレーションします。
自由空間の量子粒子の運動
1次元自由空間中の量子粒子(波束)は以下のとおりに表すことができます。
x_0:波束の中心
sigma:波束の幅
k_0:波数の中心
量子力学についての参考ページ
・量子力学のための波動論1:平面波の時間発展
・量子力学のための波動論2:平面波の重ね合わせによる波束の生成
・量子力学のための波動論3:ガウシアンパルスの時間発展
・量子力学のための波動論4:ガウシアンパルスの時間発展の解析解
シミュレーション結果
計算パラメータ
波束の中心エネルギー:E0 = 10.0 * eV;
空間スケール 1E-11[m];//横軸の値
時間スケール 1E-16[s];//動画1コマの時間間隔
考察と次の課題
・1粒子の運動は問題なく計算できている。
・2粒子の衝突をシミュレーションする。
プログラムソース(C++)
・http://www.natural-science.or.jp/files/physics/QuantumPhysics.zip
※VisualStudio2017のソルーションファイルです。GCC(MinGW)でも動作確認しています。
































