【量子力学再入門3】
無限に高いポテンシャル障壁へ衝突する量子粒子
量子力学とは原子や電子といったナノスケールにおける粒子の運動を記述する物理学の一分野です。 メートルスケールで成り立つ「ニュートンの運動方程式」に対して、量子力学では「シュレディンガー方程式」と呼ばれる基礎方程式が成り立つと考えられています。本項では量子力学の基本的な問題を数値的に解くことで、量子力学の理解を深めることが目的とします。3回目のテーマは「無限に高いポテンシャル障壁への衝突」です。
対象とする系:無限に高いポテンシャル障壁へ衝突する量子粒子
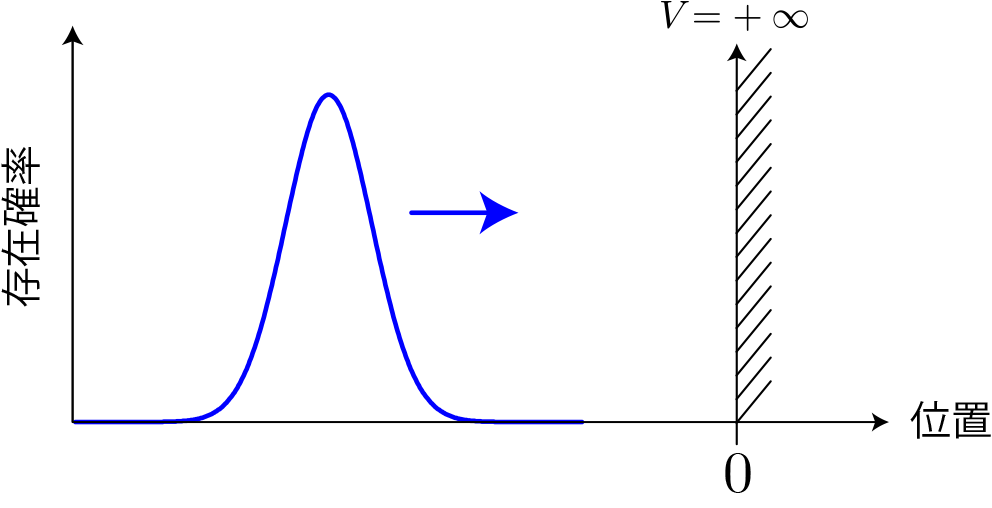
物理学におけるポテンシャルとは粒子が受ける力の源泉を意味します。ちなみにポテンシャルの空間変化の大きさが粒子に加わる力と比例関係にあります。 無限に高いポテンシャル障壁とは、ある地点から無限に高いポテンシャルが存在する状況を表しますが、この境界では粒子に無限大の強さの力が加わることを意味します。 また、ポテンシャルが無限大の領域では粒子は存在することができません。
本稿ではx>0で無限に高い壁(ポテンシャル障壁)に、x<0から量子粒子波束を衝突させるシミュレーションを行います。このようなポテンシャル障壁が存在する系でもそれぞれの領域で存在しうる平面波の重ね合わせで波束の運動をシミュレーションすることができます。
無限に高いポテンシャル障壁へ衝突する量子粒子の平面波解
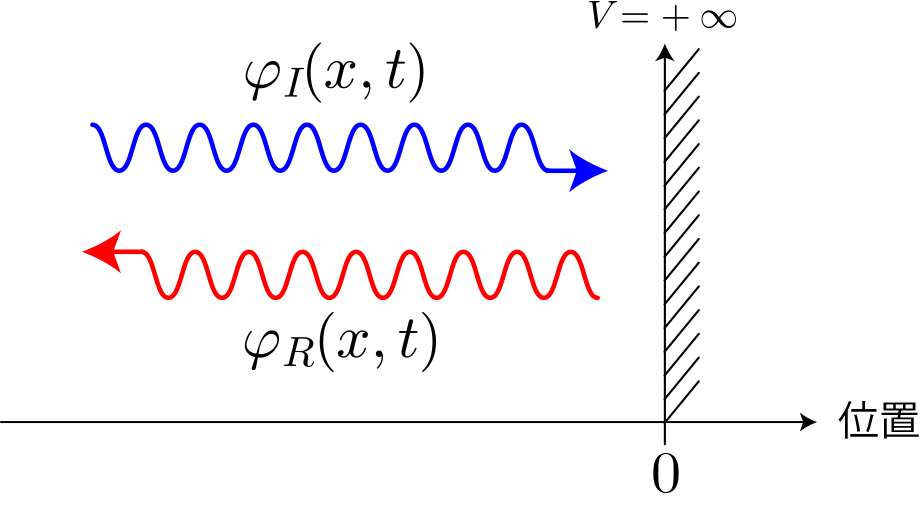
波束を生成する平面波解を導出します。
図はx>0の領域における単一角振動数の平面波の模式図です。入射波の波動関数を、反射波の波動関数を
と表した場合、トータルの波動関数はその和で表されます。
入射波の複素振幅を1とした場合の反射波の複素振幅をrとした場合、と
は
と表すことができ、トータルの波動関数は次のとおりになります。
ただし、この時点では反射波の複素振幅r(以下、反射係数と呼びます)は未定です。このrを決定するのが境界条件です。境界条件としてポテンシャルが無限大の領域では粒子の存在を表す波動関数は0になることを表す
を課します。これにより反射係数はr=-1であることがわかります。つまり、単一の平面波が存在する系の波動関数は
となることがわかりました。
無限に高いポテンシャル障壁へ衝突する量子粒子波束の運動
先に得られた平面波は波数kが異なっても元のシュレディンガー方程式を満たします。そのため、異なる波数(角振動数)をもつ平面波を重ね合わせてた波動関数も元のシュレディンガー方程式を満たします。そのため、無限に高いポテンシャル障壁が存在する場合でも、平面波の重ね合わせで波束の運動を調べることができます。異なる波数(角振動数)をもつ平面波を次のとおりです。
ただし、エネルギーと角振動数、波数の関係性(分散関係)は以下のとおりです。
シミュレーション結果
初期状態として左から右向きに運動する波束の運動です。
計算パラメータ
波束の中心エネルギー:E0 = 10.0 * eV;
空間スケール 1E-11[m];//横軸の値
時間スケール 1E-16[s];//動画1コマの時間間隔
考察と次の課題
・無限に高いポテンシャル障壁への衝突は問題ないようだ
・次はステップ関数型ポテンシャル障壁への衝突をシミュレーションしてみます。
プログラムソース(C++)
・http://www.natural-science.or.jp/files/physics/QuantumPhysics3.cpp
※VisualC++、GCC(MinGW)で動作確認しています。
































