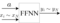【ニューラルネットワークの基礎研究21】
重みの初期値依存性
ニューラルネットワークの自由度は各ユニットごとに与えられたバイアスと、各ユニット間をつなぐ重みです。これまで、重みは平均を0、絶対値の最大値を\sqrt(6.0/unit数)とするランダムな値を与えていました(Heの初期値)。今回は重みの初期値を小さくしてみます。具体的には0.9倍, 0.7倍, 0.5倍, 0.3倍, 0.1倍を同一条件で比較してみます。
対象とする関数は三角関数です。
【これまでの結果】
→ 1変数の2次関数の学習 1 2 3 4
→ 係数が変化する2次関数の学習 1 2 3 4
→ べきが変化するべき関数の学習 1 2 3
→ 学習効果を高めるにはディープ(層数)と並列数(ユニット数)のどちらが有効か?
→ 底が変化する指数関数の学習 1 2 3
→ 関数形ごとの学習成果の比較
→ 角振動数が変化する三角関数の学習 1 2
→ 関数の入力数と出力数を一致させた構造 1 2
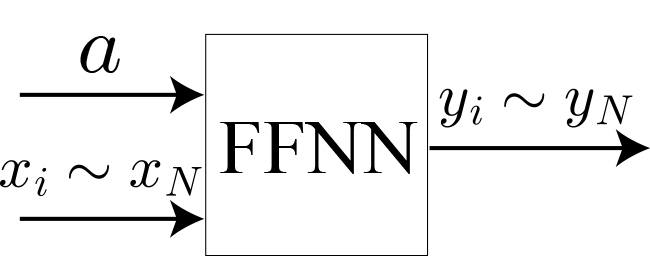
ニューラルネットワークの基本パラメータ
・ニューラルネットワークの構造:順伝播型ニューラルネットワーク(FFNN)
・学習方法:通常の勾配法(学習率固定、逆誤差伝搬法)
・学習率:eta = 0.01;
・ミニバッチ数:100 (サンプルは無限に用意できるためミニバッチという概念は存在しませんが、ランダムに用意したミニバッチ数分のサンプルに対する平均を用いて学習を進める)
・活性化関数(中間層):ReLU(ランプ関数)
・活性化関数(出力層):恒等関数
・損失関数:2乗和
※独立したネットワークを10個用意してそれぞれ個別に学習させて、学習効果の高かった上位5つの「学習回数」vs「損失値」をグラフ化します。
※参考ページ
中間層のユニット数100で4層のニューラルネットワーク(102-100-100-100-100-101)
0.9倍
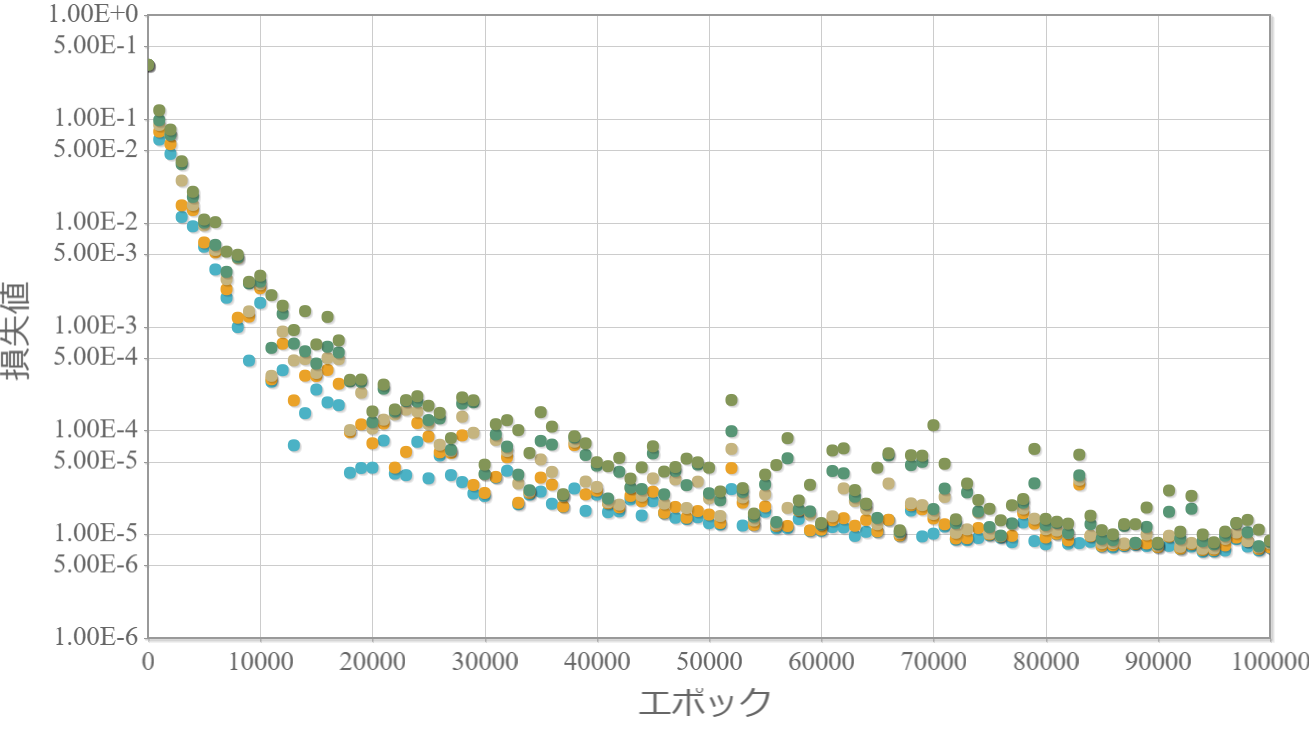
0.7倍
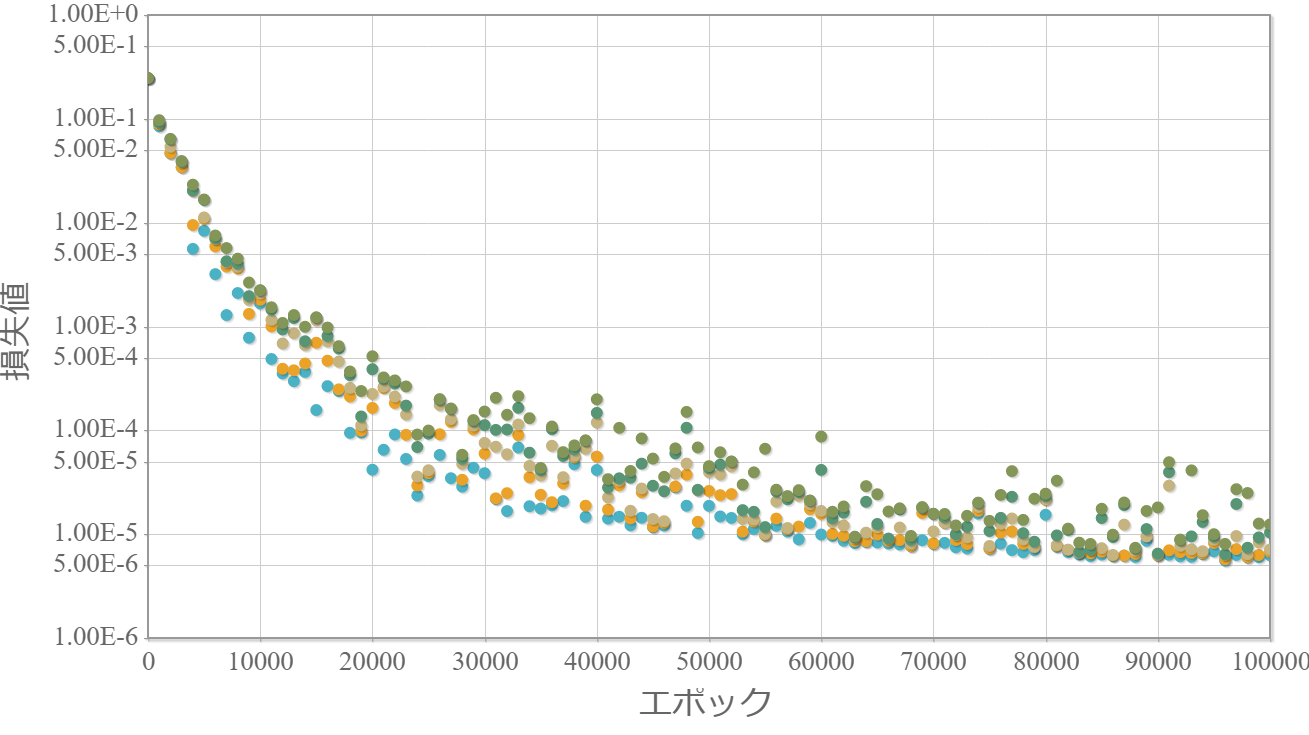
0.5倍
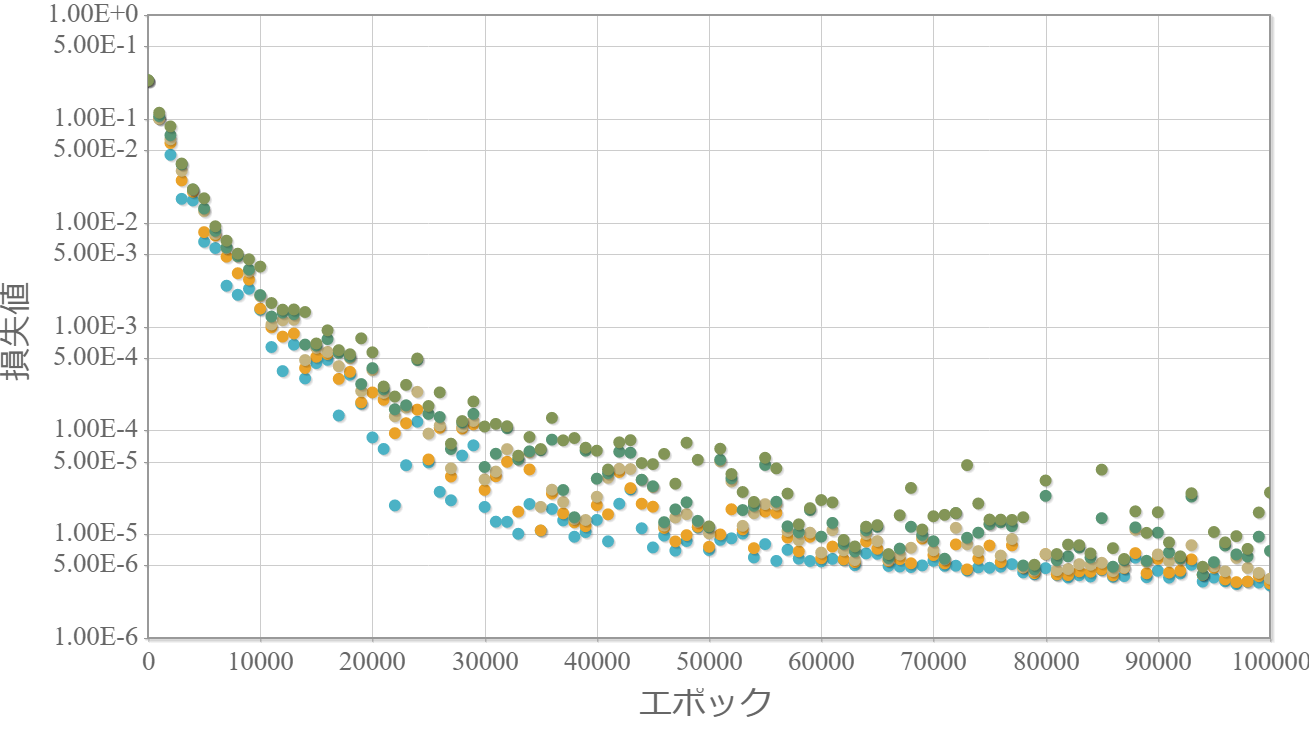
0.3倍
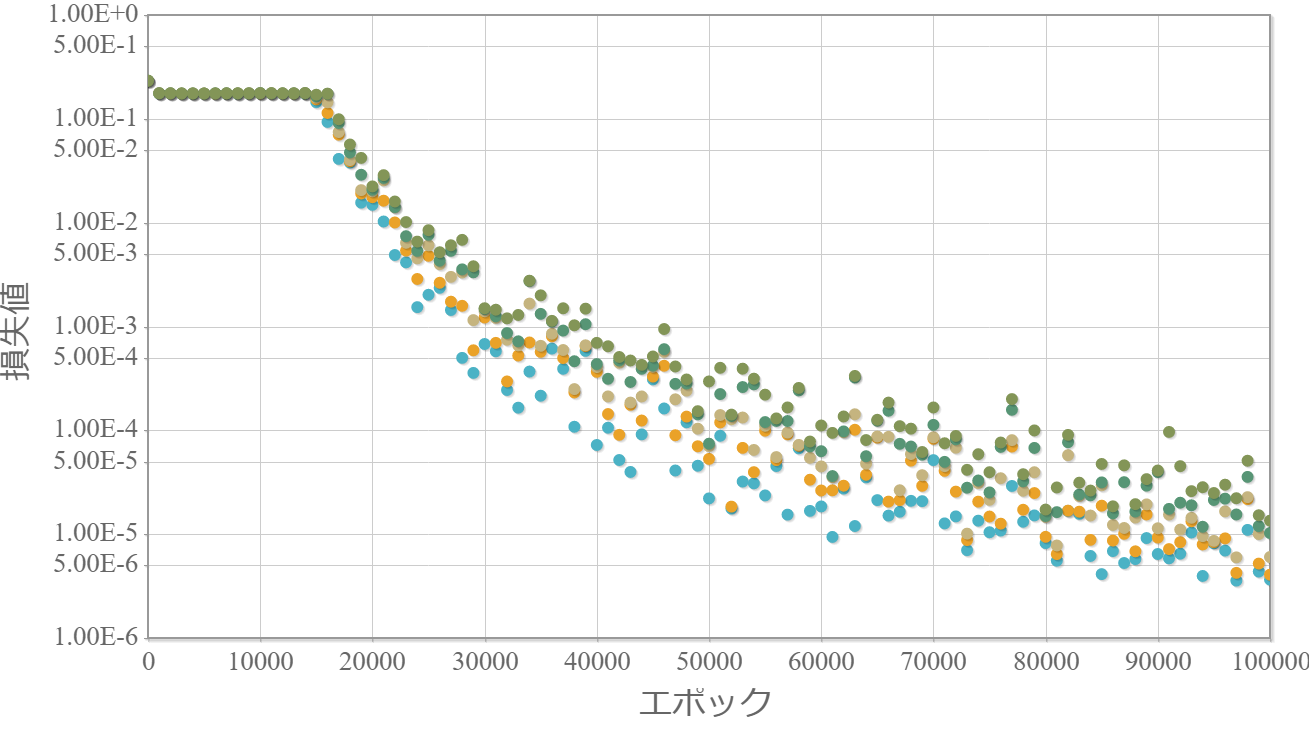
0.1倍
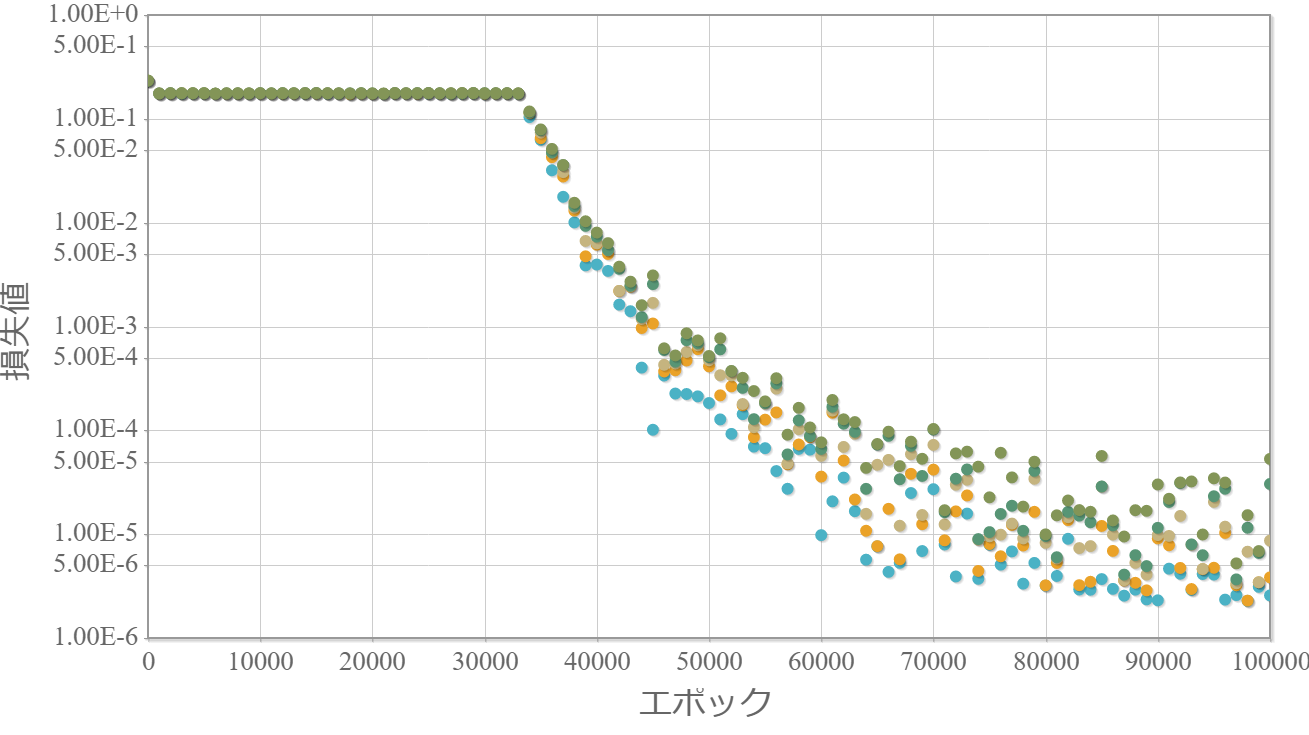
考察と次の課題
・重みは小さい方が最終的な学習効果は高い。
・0.3倍と0.1倍でははじめ学習が進んでいないが、学習の過程である程度の重みの大きさになった途端、学習が進んでいる。
→ 学習が進む最低な重みが存在する
・はじめは大きめな重みを与えておいて、損失関数にて重みの大きさに応じたペナルティを与えることで、ちょうど良い重みへ誘導できるかもしれない。
次の課題
・損失関数にLASSO回帰因子によるペナルティを加えて、学習を開始した序盤に重みを抑える方法を導入してみる。
プログラムソース(C++)
・http://www.natural-science.or.jp/files/NN/FFNNs_epoch_Functions2.zip
※VisualStudio2017のソルーションファイルです。GCC(MinGW)でも動作確認しています。