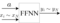【ニューラルネットワークの基礎研究22】
重み減衰のためにLASSO回帰因子を与えてみる
前回の実験では、重みは初期値は多く過ぎても小さすぎてもだめであることが確認できました。
そこで、重みをちょうど良い大きさへ減衰させるために、損失関数にLASSO回帰因子によるペナルティを加えて、学習を開始した序盤に重みを抑える方法を導入してみます。
比較対象として、中間層のユニット数100で4層のニューラルネットワーク(102-100-100-100-100-101)を用意して、重みの初期値の範囲を-1から1までランダムに与え、LASSO回帰因子を0.05, 0.005, 0.0005と与えて変化を見てみます。
【これまでの結果】
→ 1変数の2次関数の学習 1 2 3 4
→ 係数が変化する2次関数の学習 1 2 3 4
→ べきが変化するべき関数の学習 1 2 3
→ 学習効果を高めるにはディープ(層数)と並列数(ユニット数)のどちらが有効か?
→ 底が変化する指数関数の学習 1 2 3
→ 関数形ごとの学習成果の比較
→ 角振動数が変化する三角関数の学習 1 2
→ 関数の入力数と出力数を一致させた構造 1 2
→ 重みの初期値依存性
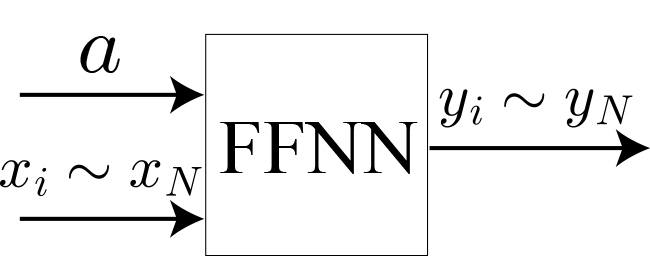
ニューラルネットワークの基本パラメータ
・ニューラルネットワークの構造:順伝播型ニューラルネットワーク(FFNN)
・学習方法:通常の勾配法(学習率固定、逆誤差伝搬法)
・学習率:eta = 0.01;
・ミニバッチ数:100 (サンプルは無限に用意できるためミニバッチという概念は存在しませんが、ランダムに用意したミニバッチ数分のサンプルに対する平均を用いて学習を進める)
・活性化関数(中間層):ReLU(ランプ関数)
・活性化関数(出力層):恒等関数
・損失関数:2乗和
※独立したネットワークを10個用意してそれぞれ個別に学習させて、学習効果の高かった上位5つの「学習回数」vs「損失値」をグラフ化します。
※参考ページ
中間層のユニット数100で4層のニューラルネットワーク(102-100-100-100-100-101)
LASSO回帰因子:0.05
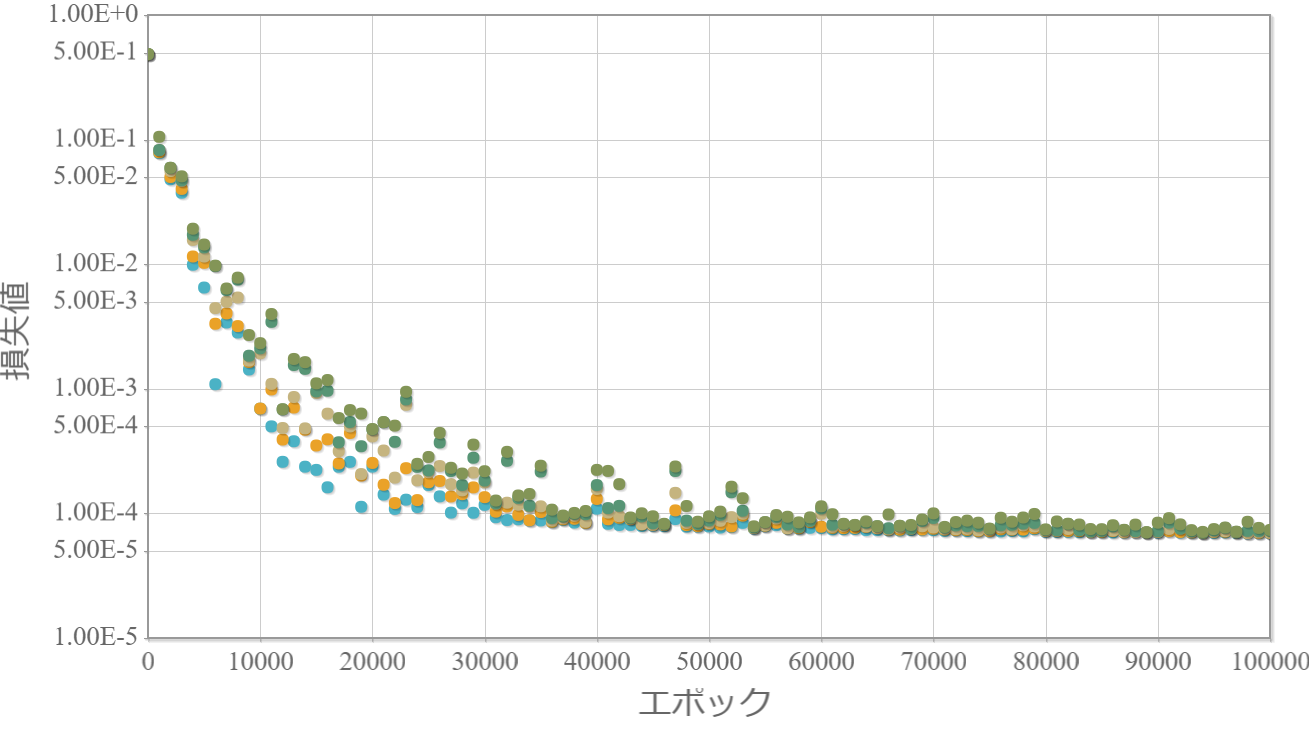
LASSO回帰因子:0.005
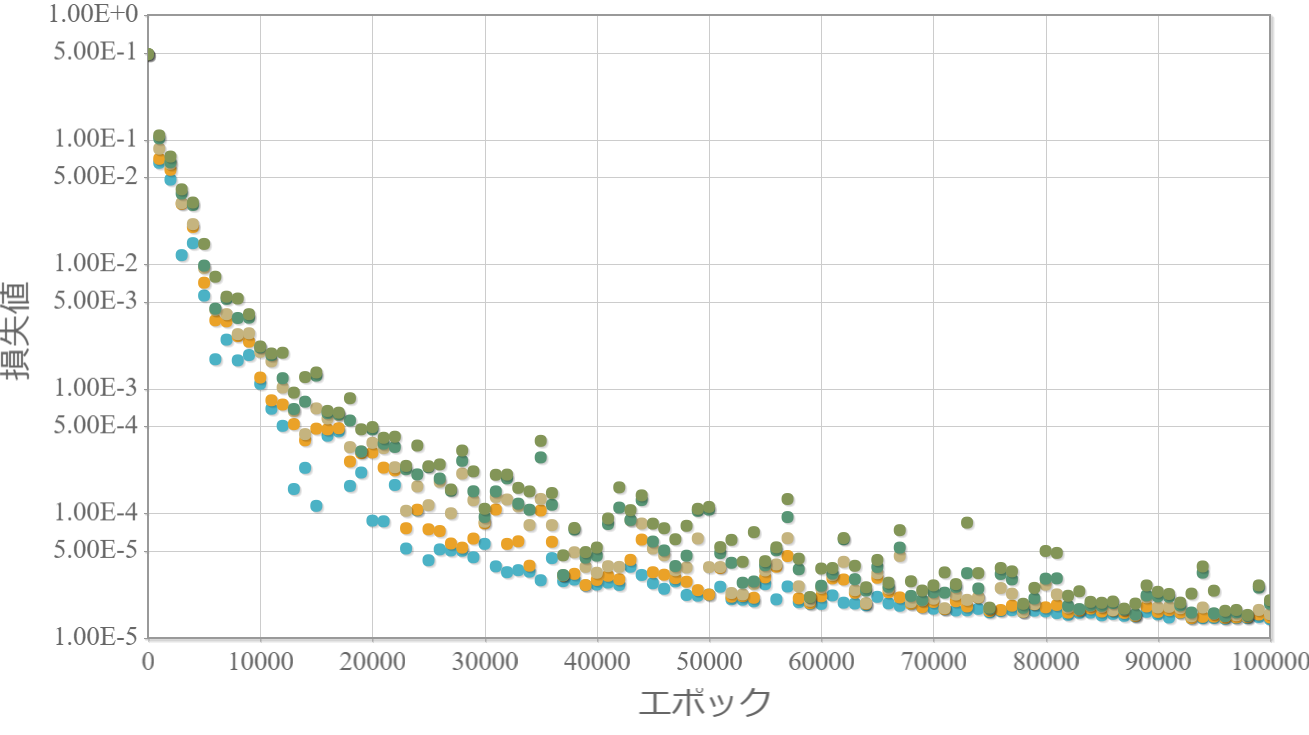
LASSO回帰因子:0.0005
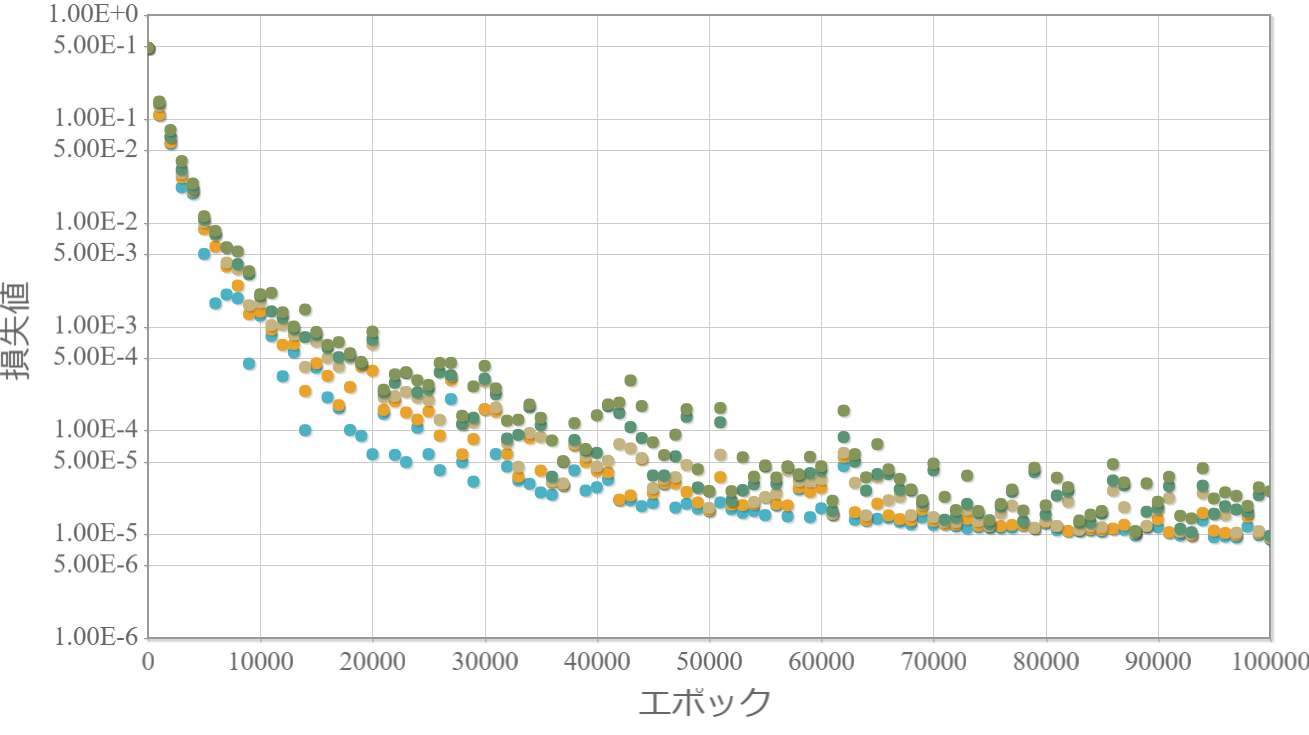
考察と次の課題
・LASSO回帰因子の大きさによって損失値の下限が収束する様子がわかる。
→ LASSO回帰因子を単純に導入しただけでは重みの大きさの最適化は難しそうだ。
次の課題
・LASSO回帰因子を学習回数に応じて変化させてみる。
プログラムソース(C++)
・http://www.natural-science.or.jp/files/NN/FFNNs_epoch_Functions2.zip
※VisualStudio2017のソルーションファイルです。GCC(MinGW)でも動作確認しています。