【ニューラルネットワークの基礎研究27】
放物運動の粘性抵抗係数と初速度と投射角度から飛距離を学習してみる
「解析解は得られないが数値解が容易に得られる系で、学習の成果を簡単に検証できる問題」として、空気抵抗力が存在する放物運動を対象として物理的な運動を学習させています。
前々回と前回では、放物運動の軌跡から粘性抵抗係数と慣性抵抗係数を学習させました。今回はアプローチを変えて、粘性抵抗係数・入射角度・初速度を与えて、その時の飛距離を学習させてみます。

ニューラルネットワークの基本パラメータ
・ニューラルネットワークの構造:順伝播型ニューラルネットワーク(FFNN)
・学習方法:通常の勾配法(学習率固定、逆誤差伝搬法)
・学習率:eta = 0.01;
・ミニバッチ数:100 (サンプルは無限に用意できるためミニバッチという概念は存在しませんが、ランダムに用意したミニバッチ数分のサンプルに対する平均を用いて学習を進める)
・活性化関数(中間層):ReLU(ランプ関数)
・活性化関数(出力層):恒等関数
・損失関数:2乗和
※独立したネットワークを10個用意してそれぞれ個別に学習させて、学習効果の高かった上位5つの「学習回数」vs「損失値」をグラフ化します。
中間層1層のニューラルネットワーク(200-200-2)
3-100-1
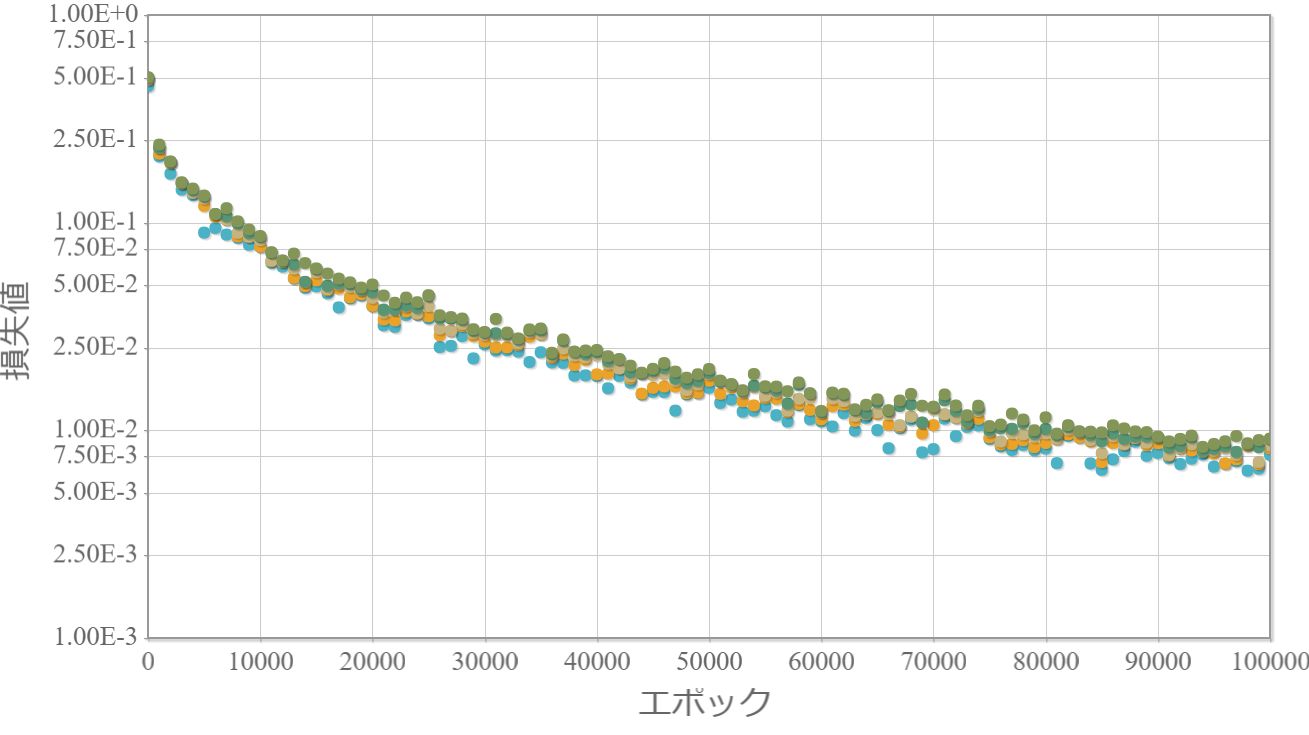
3-200-1
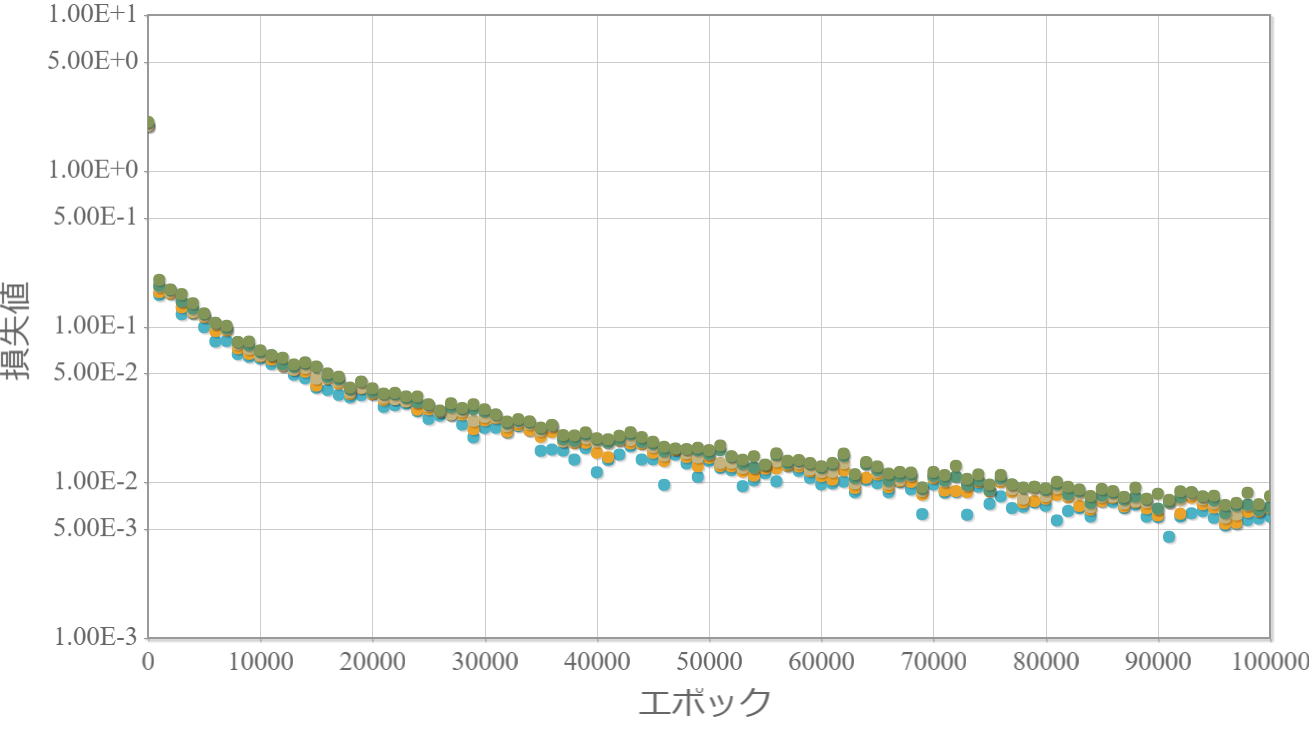
3-1000-1
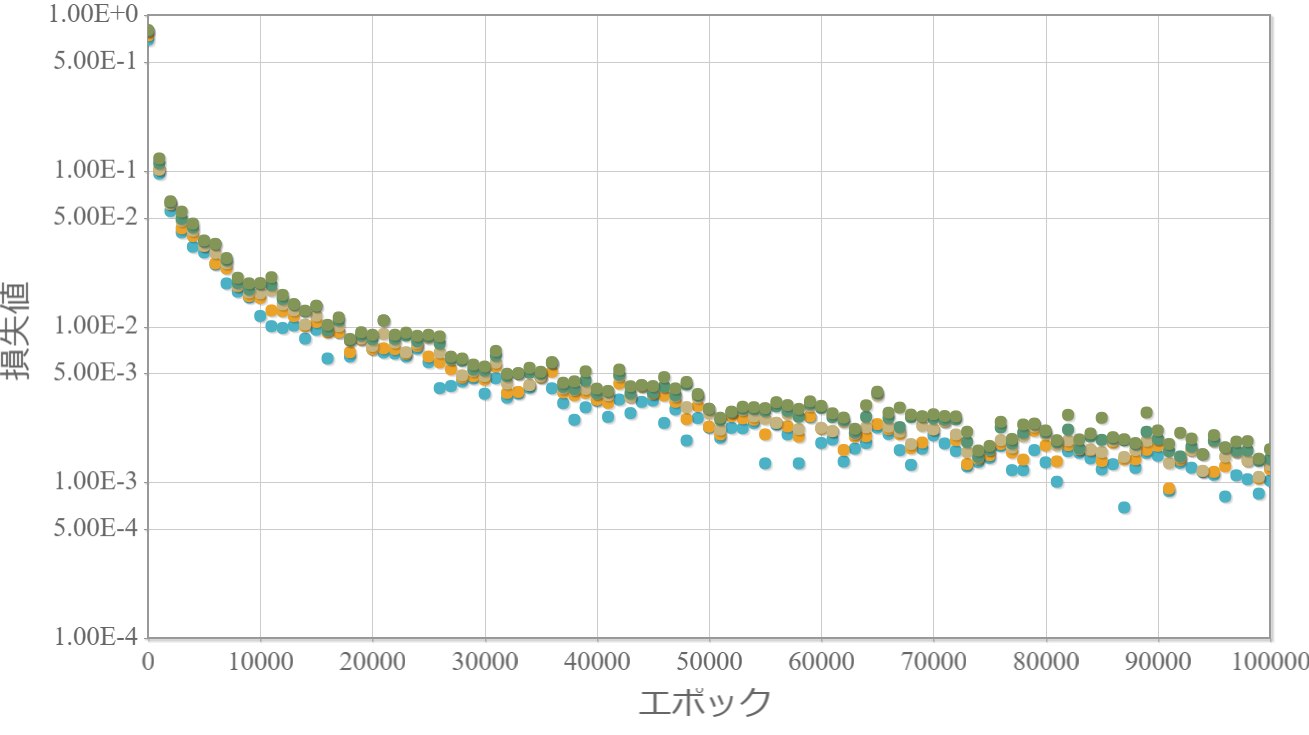
3-100-100-1
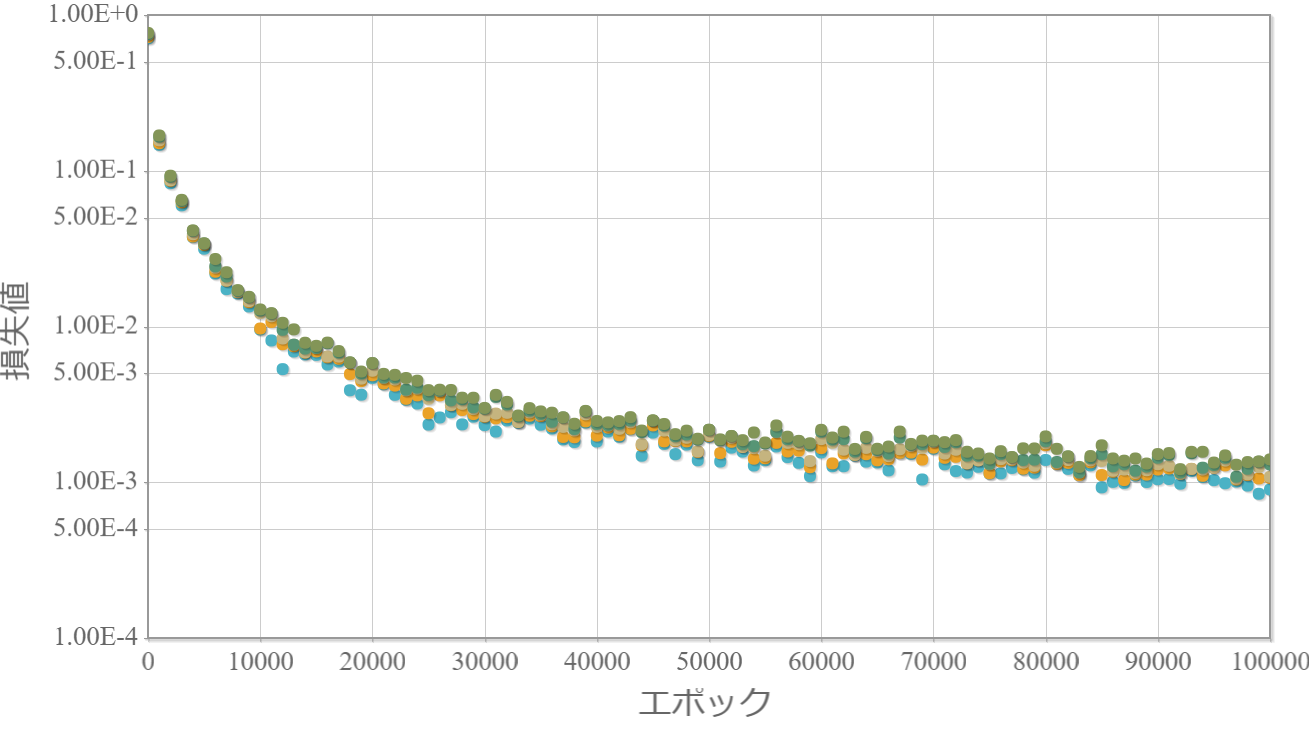
3-100-100-100-1
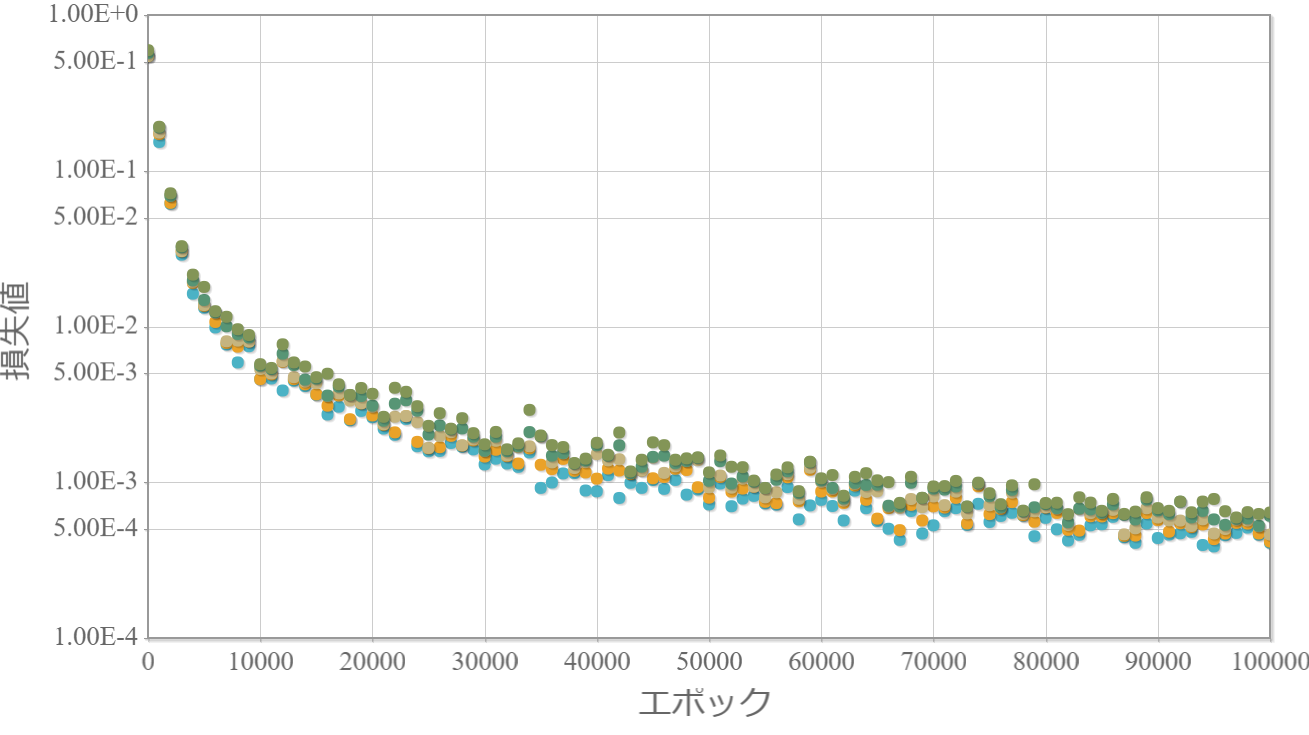
3-100-100-100-100-1
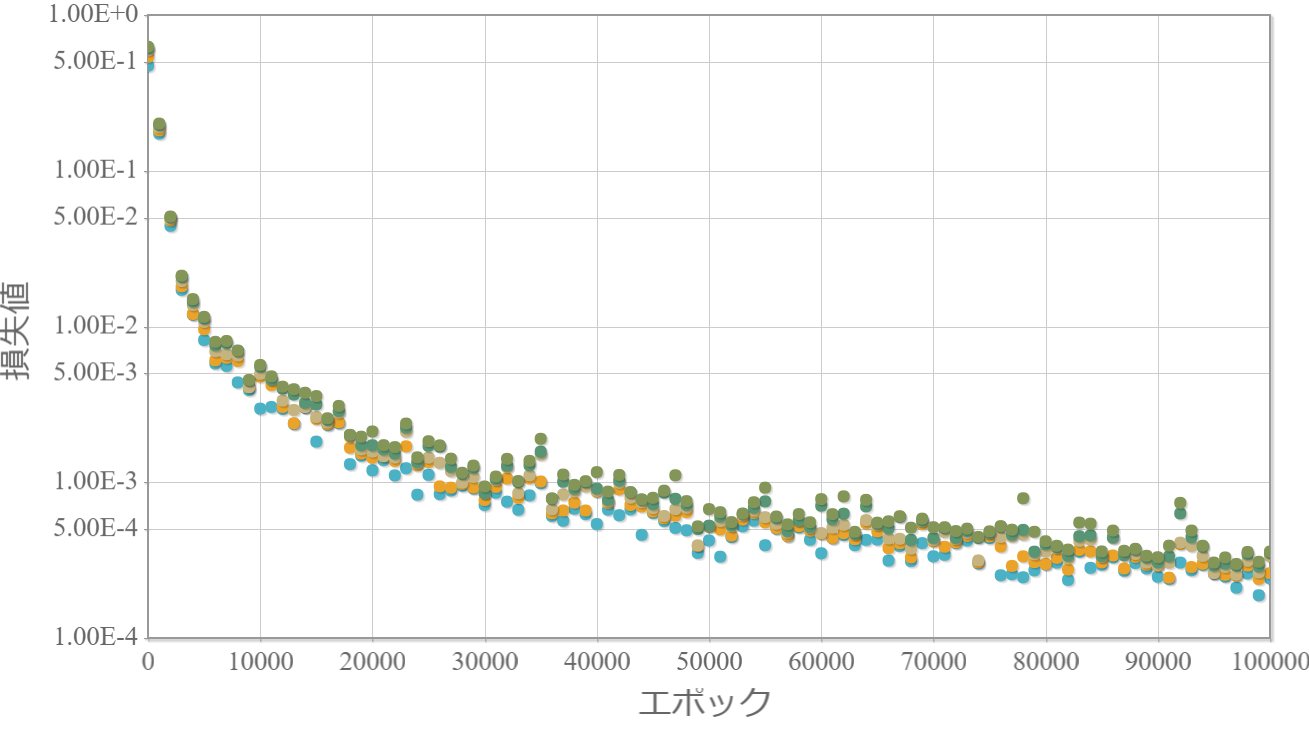
3-100-100-100-100-100-1
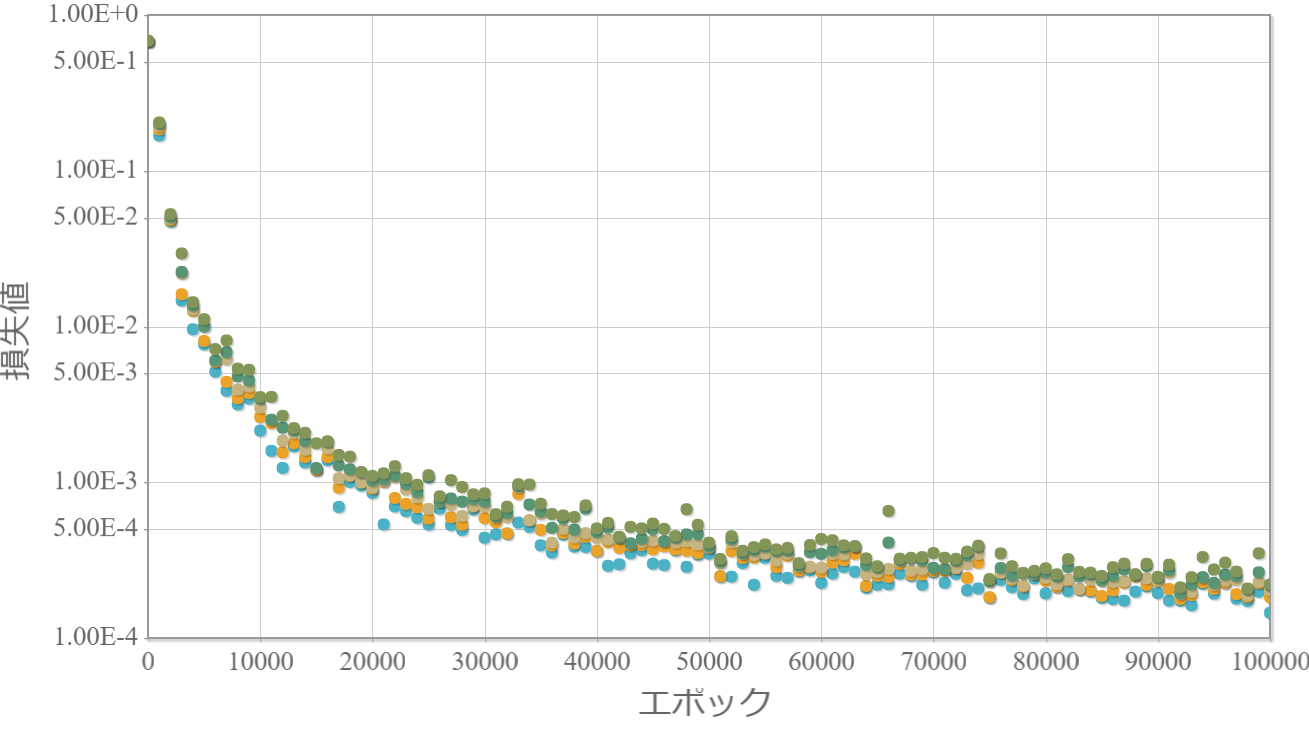
3-100-100-100-100-100-100-1
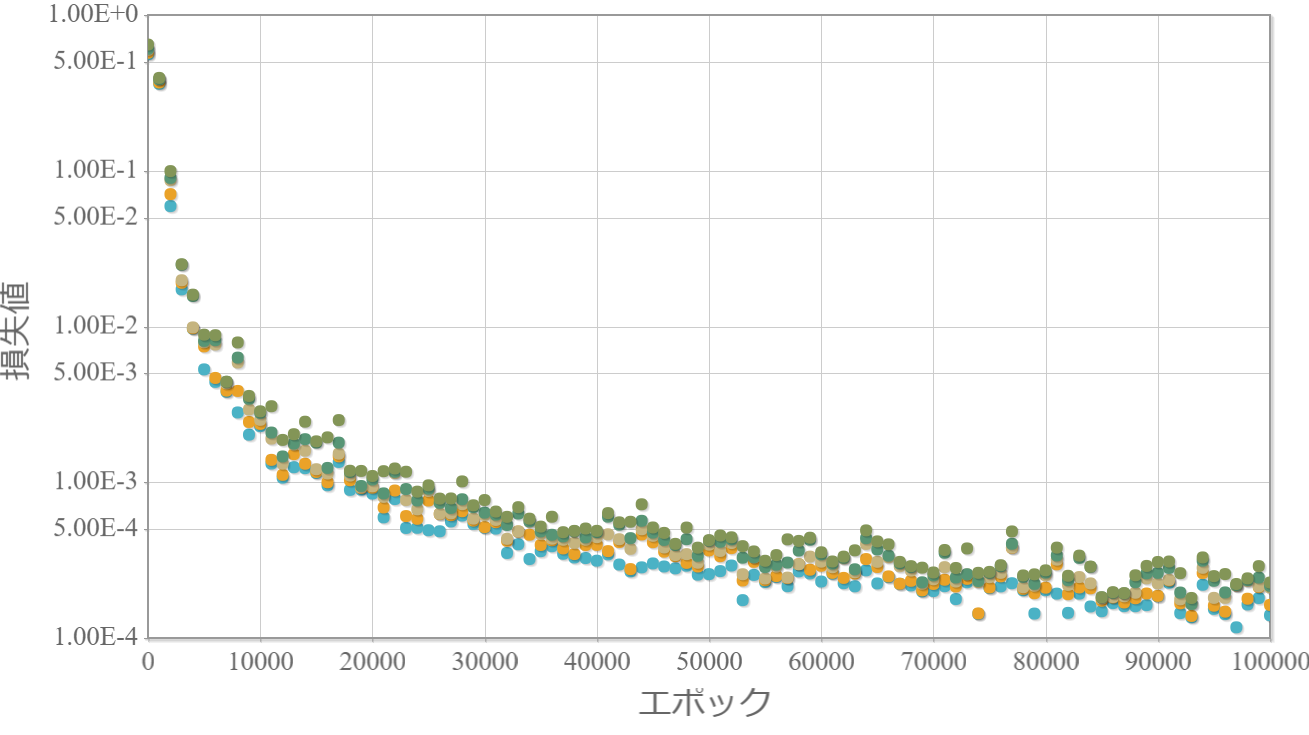
100,000回学習後のチェック
初速度20、粘性抵抗係数を0, 0.5, 1.0, 1.5として、投射角度を0°から90°までの飛距離の数値計算結果(実線)と、ネットワークによる出力をグラフ化した結果です。
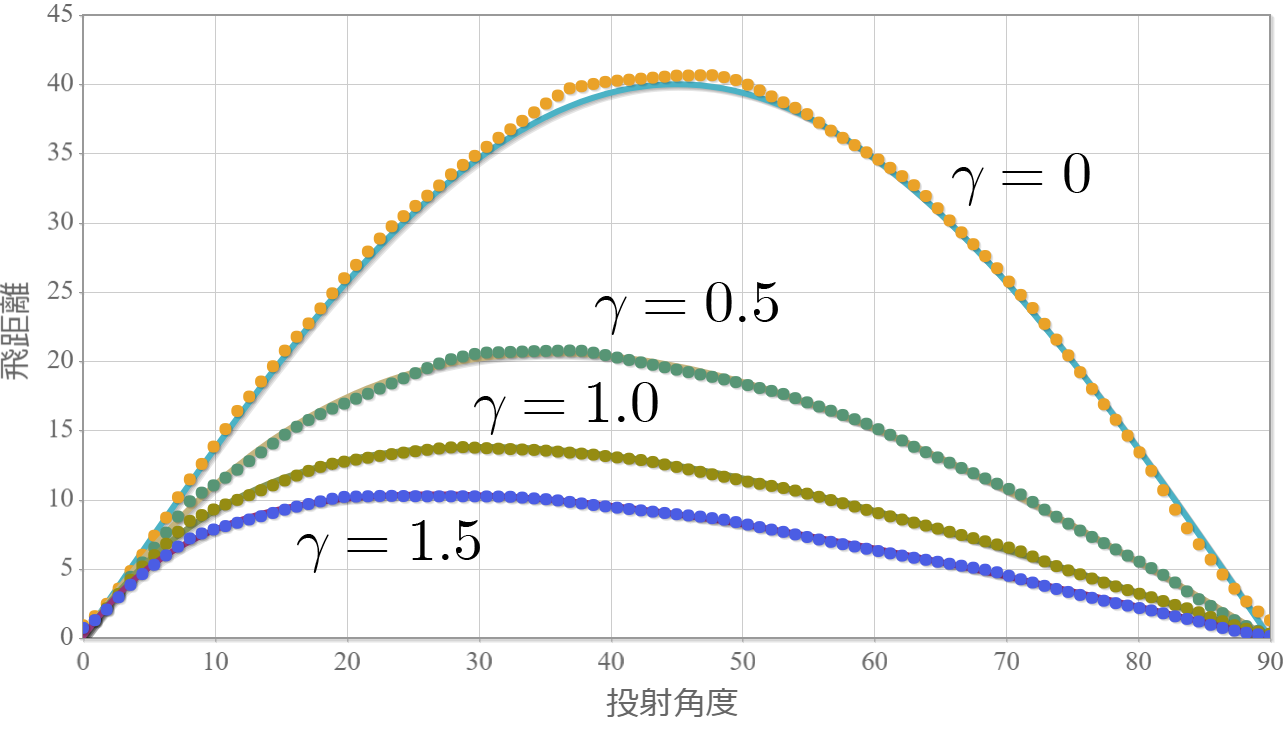
考察と次の課題
・実質的に3変数関数の学習なので問題なさそう。
・ここまでの学習でできることをまとめると以下のとおりです。
(1)軌跡から粘性抵抗係数を見積もることができる。
(2)その粘性抵抗係数を用いて初速度と投射角度を与えるとその飛距離がわかる。
(3)その結果、最大飛距離となる初速度に対する投射角度を予測できる。
・次回は入力と出力の関係を変えてみて学習させてみます(例:)。
プログラムソース(C++)
・http://www.natural-science.or.jp/files/NN/FFNNs_epoch_ProjectileMotion_AirResistance2.zip
※VisualStudio2017のソルーションファイルです。GCC(MinGW)でも動作確認しています。