【量子力学再入門11】
シュレディンガー方程式の数値解法（スペクトル法）の苦手な計算

スペクトル法はシュレディンガー方程式中の波動関数とポテンシャル項の空間分布をフーリエ級数展開して、波動関数の波数展開係数の時間発展を数値的に計算します。 その際にポテンシャル項の空間依存性のフーリエ級数展開の収束が遅い場合には、真の解からのズレが大きくなってしまいます。その最も単純な例は、これまでに解析解を用いてシミュレーションした箱型ポテンシャル障壁のような空間変化が急激な場合です。 本稿では、解析解とのズレをみてみます。

ポテンシャル項のフーリエ級数展開

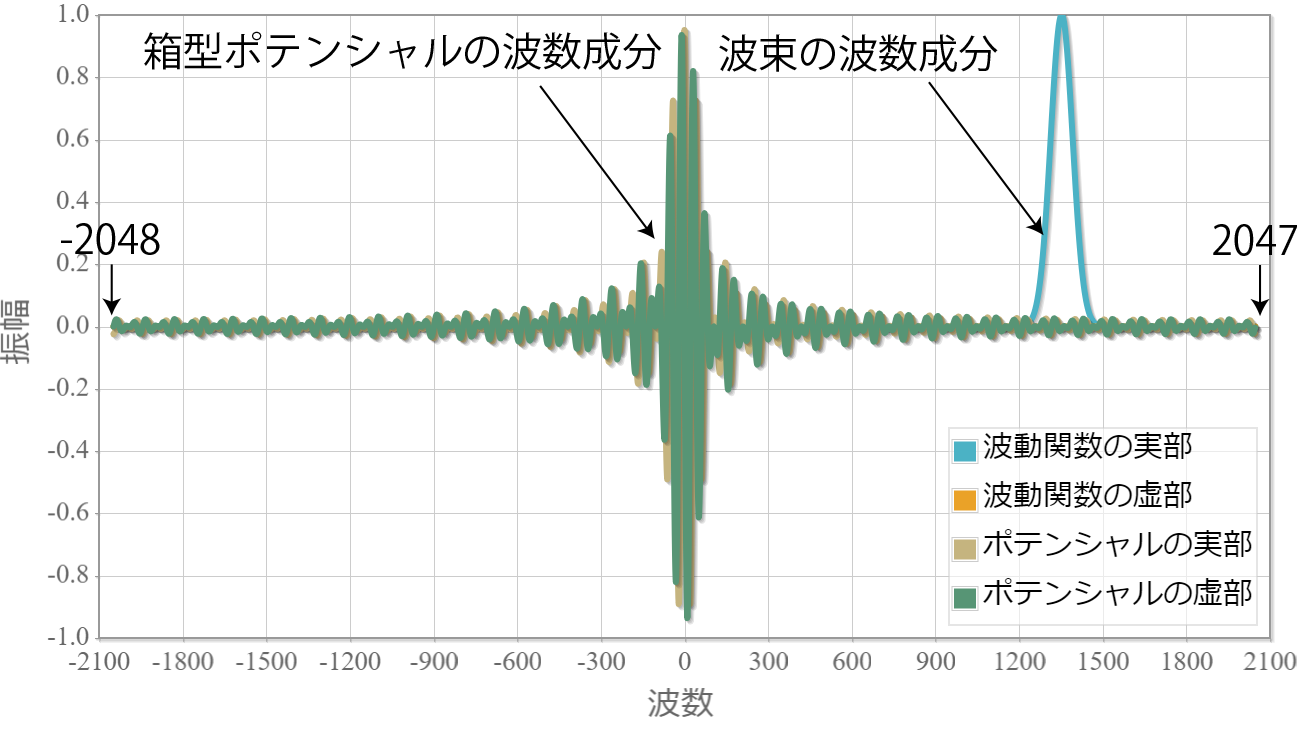
次の図は、幅500E-11[m]、高さ2.0eV、左端の位置1000E-11[m]の箱型ポテンシャルと、波動関数の初期状態のフーリエ級数展開の展開係数です。横軸が波数に対応し、縦軸が展開係数です。高さはそれぞれ適当にスケールさせています。先述のとおりですが、箱型ポテンシャルは空間的に折れ線的な変化となるため、展開係数の収束が遅く、このスケールで見ても両端ではまだ収束していません。

時間発展の計算結果

解析解と数値解を同時に描画しています。シミュレーションそのものは問題なさそうですが、反射波の見ると振幅がおよそ２倍程度も異なっています。

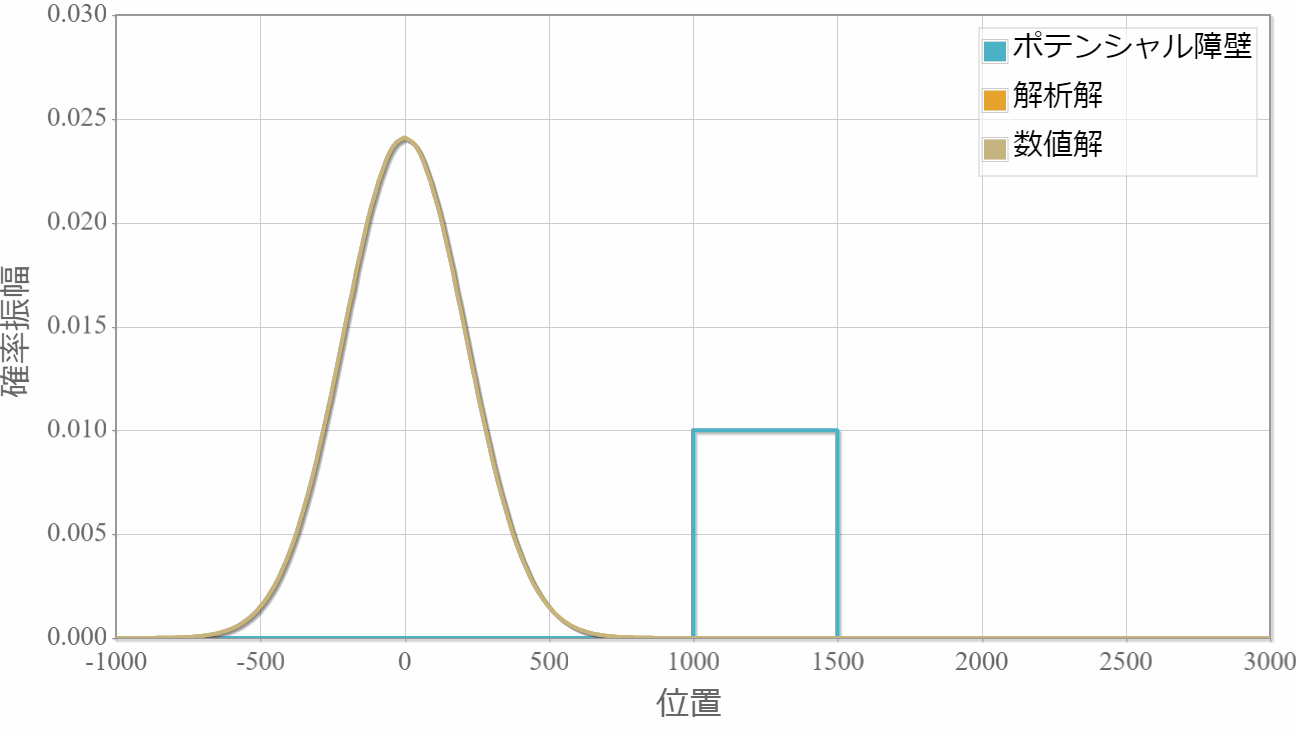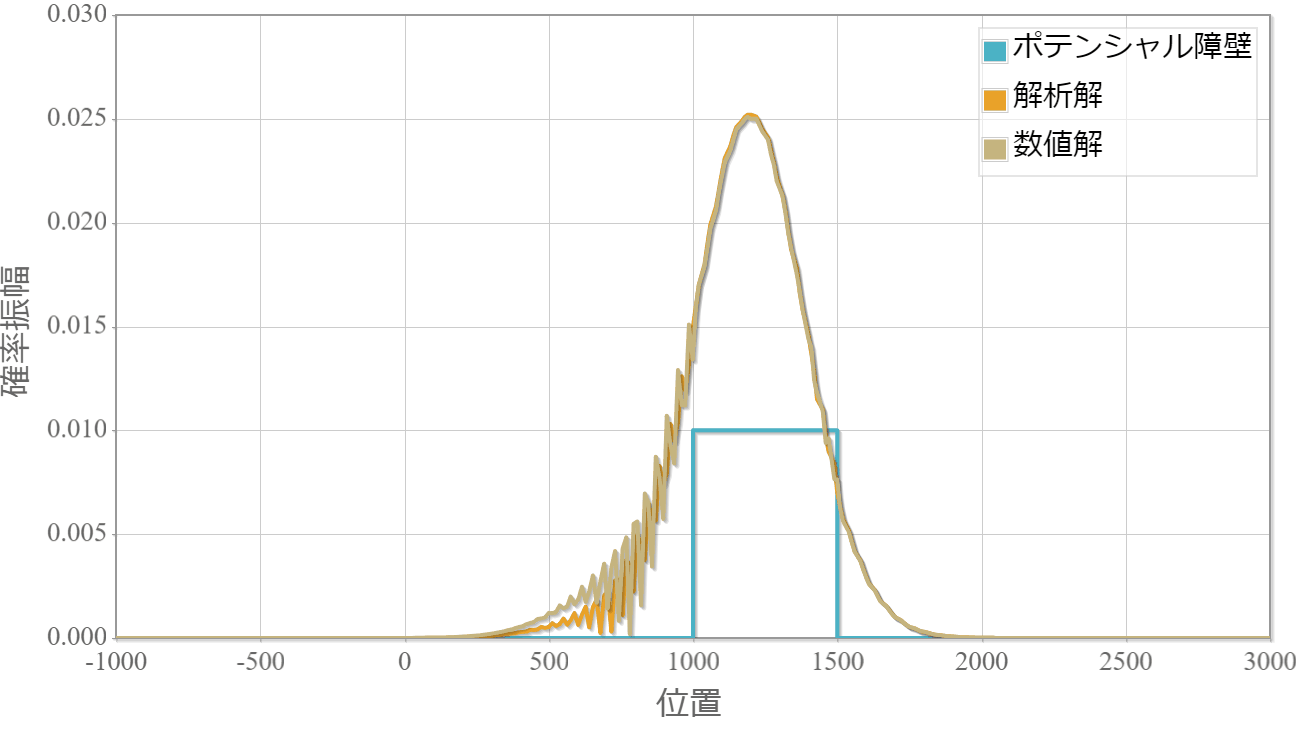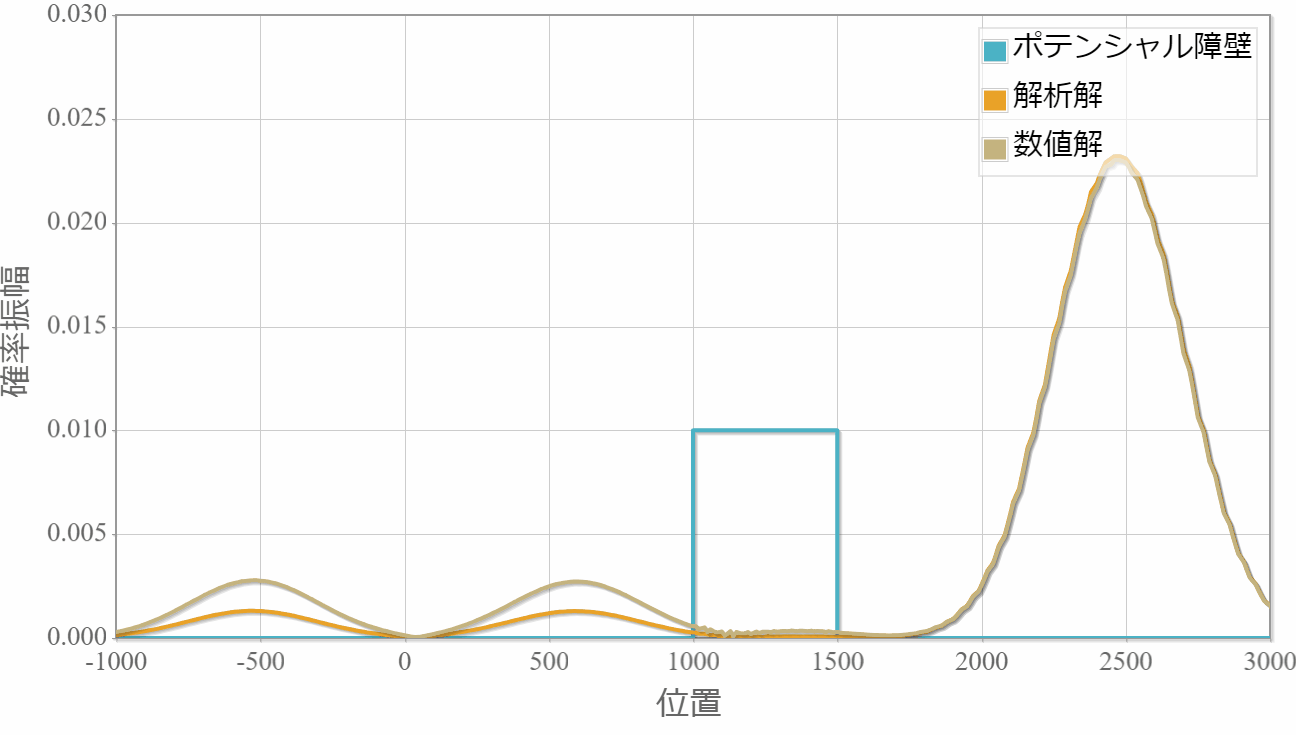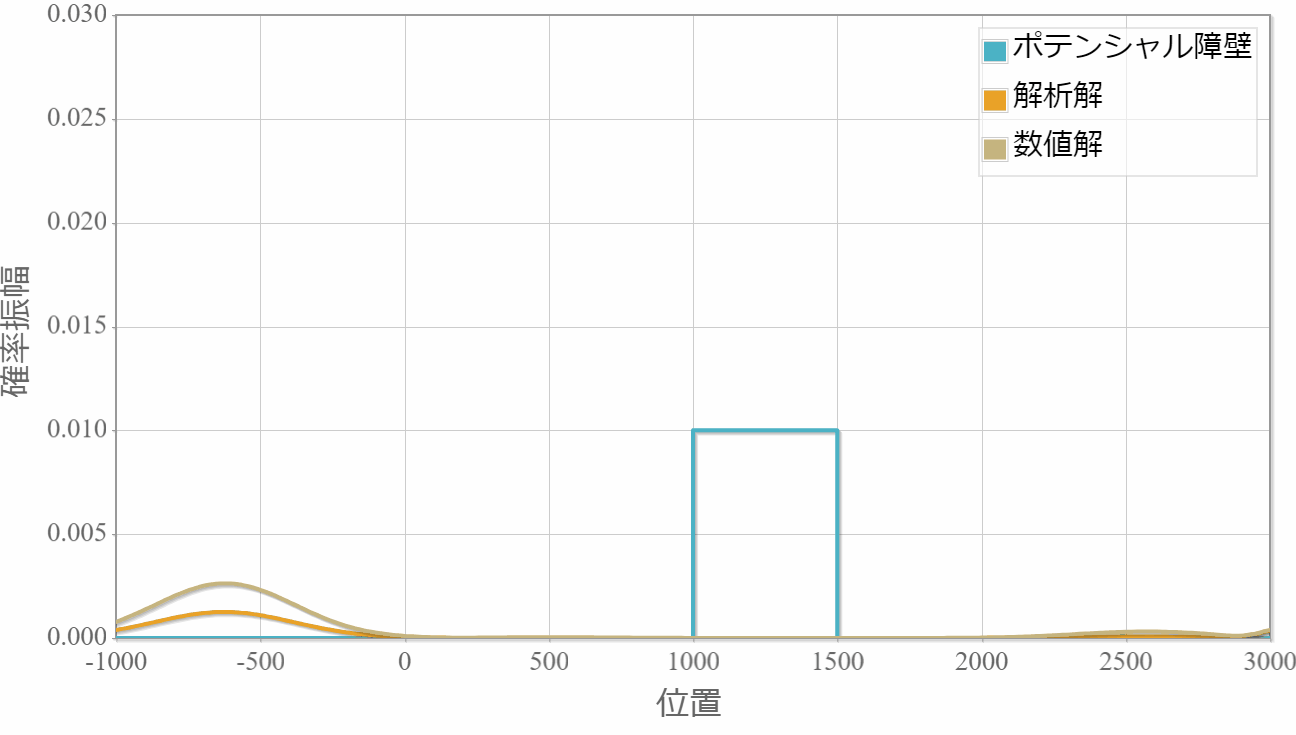
時間スケール：5E-16[s]（１コマ）
空間スケール：1E-11[m]
波束を生成する平面波の項数：500
フーリエ級数展開係数の項数：4096
ルンゲ・クッタの時間刻み幅：1.0E-18[s]

透過係数と反射係数の解析解

次の図は、波束の時間発展の解析解を計算するために用いた透過係数と反射係数の波数依存性です。波数がおよそ-600から600の間は透過率が０（反射率が１）の領域で、その両端で激しく振動しているのは共鳴透過です。

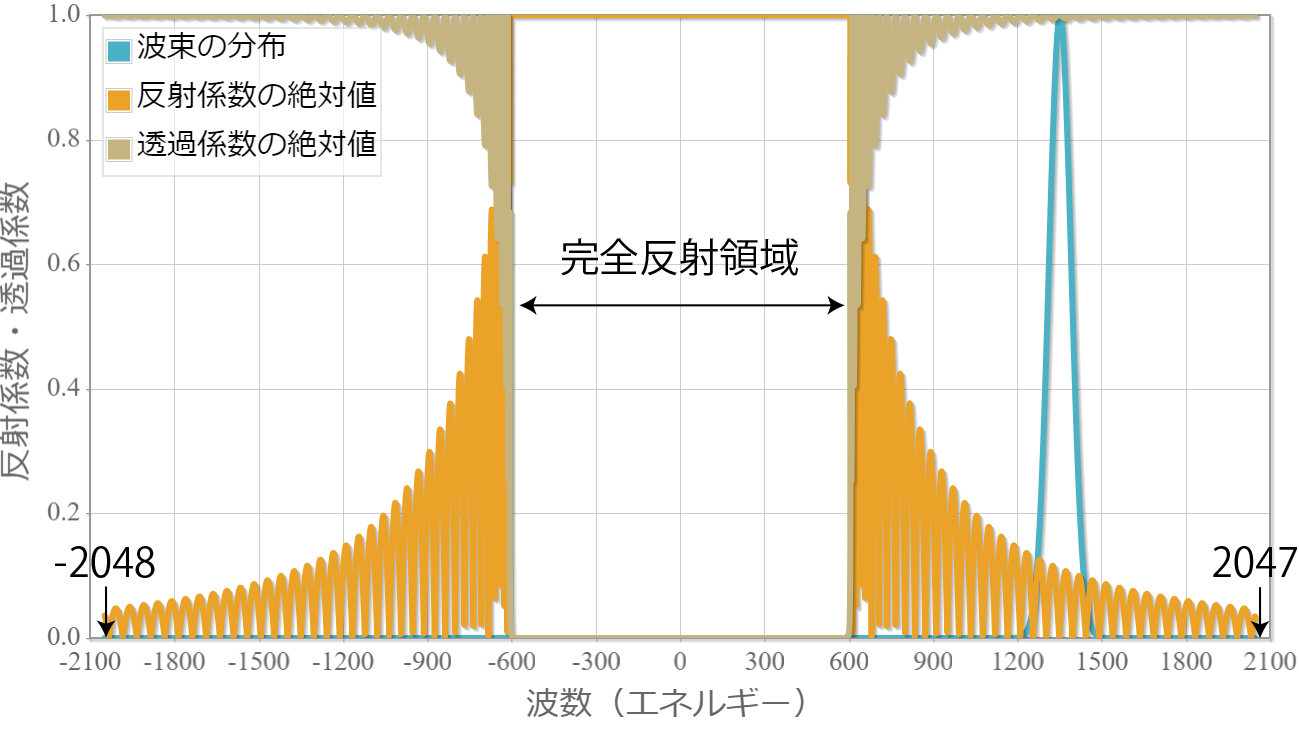
プログラムソース（C++）

・http://www.natural-science.or.jp/files/physics/QuantumPhysics_OpenMP11.cpp
※VisualC++、GCC（MinGW）で動作確認しています。