【量子力学再入門12】
井戸型ポテンシャル中の波束の運動（スペクトル法）
文責：遠藤 理平 （2018年5月21日）
カテゴリ：計算物理学(165)
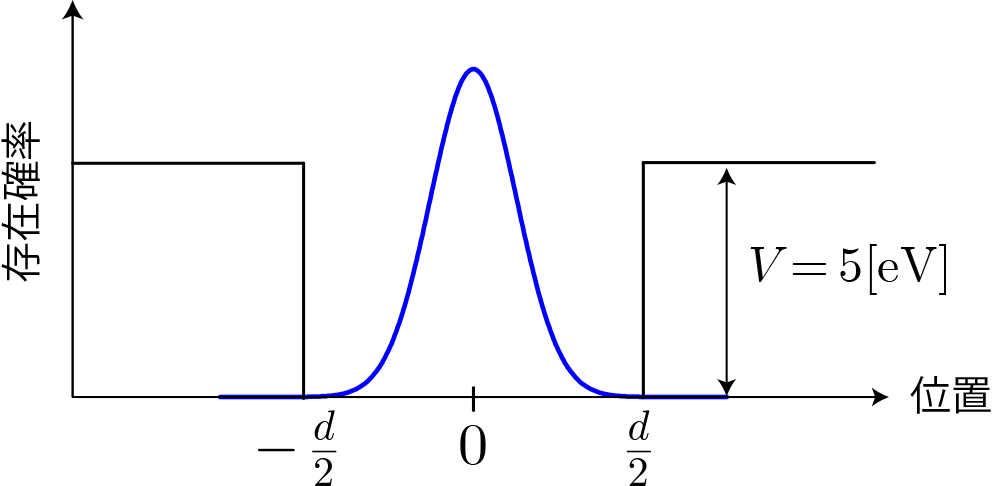
スペクトル法を用いた例として、下図のような井戸型ポテンシャル中の波束の運動を数値計算して見ましょう。 波束の中心エネルギーは０で、井戸の高さは波束を構成するエネルギーより大きいとします。
ポテンシャル項のフーリエ級数展開
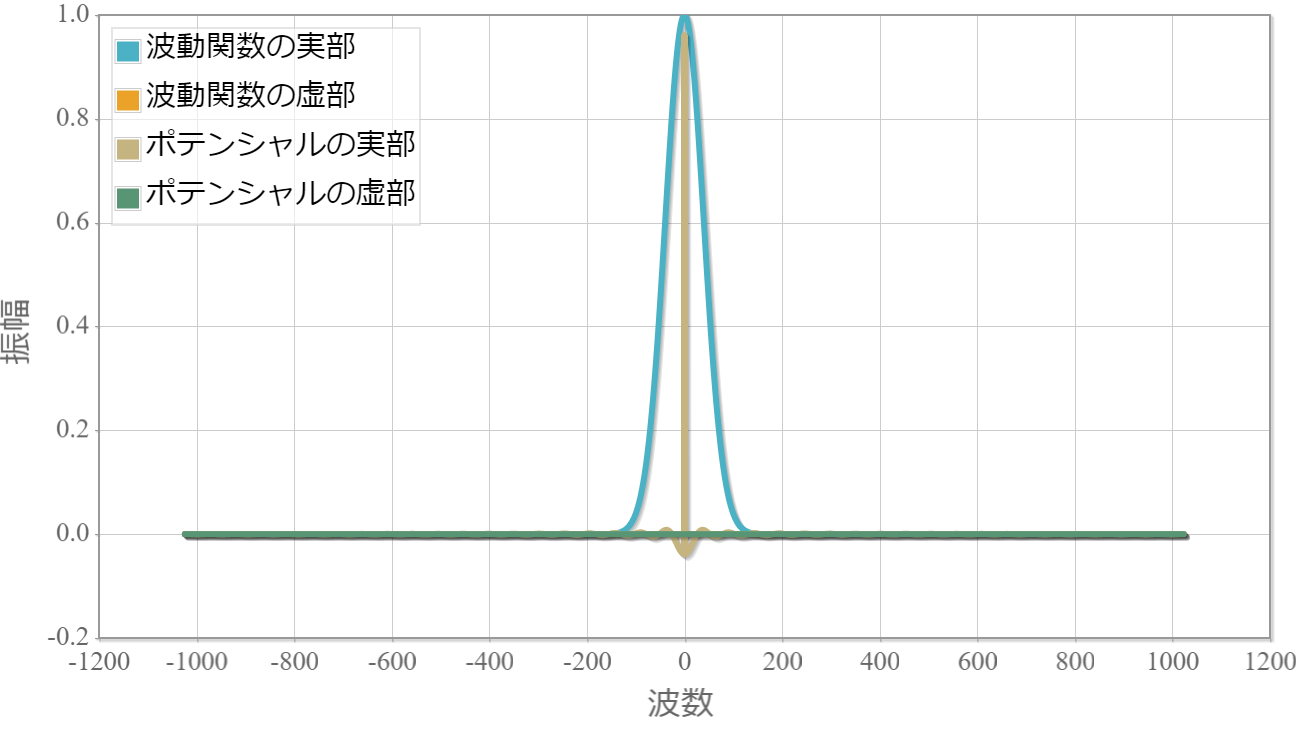
次の図は、幅2000E-11[m]、高さ5.0eVの井戸型ポテンシャルと、波動関数の初期状態のフーリエ級数展開の展開係数です。横軸が波数に対応し、縦軸が展開係数です。高さはそれぞれ適当にスケールさせています。幅の広い井戸型ポテンシャルの場合、フーリエ級数展開の収束が思いのほか早いです。
時間発展の計算結果
波束を構成するエネルギーよりも井戸の深さが深いため、波束は井戸の外には漏れ出すことなく周期的な運動を行っています。
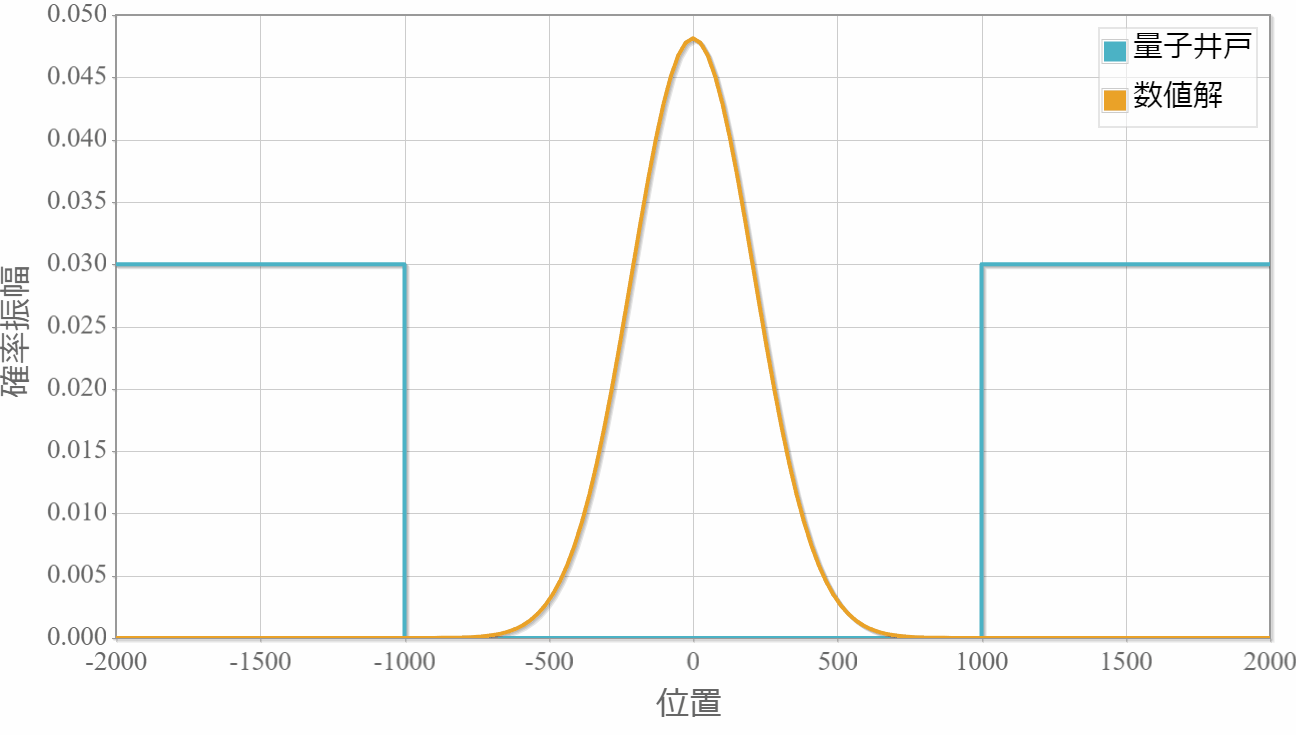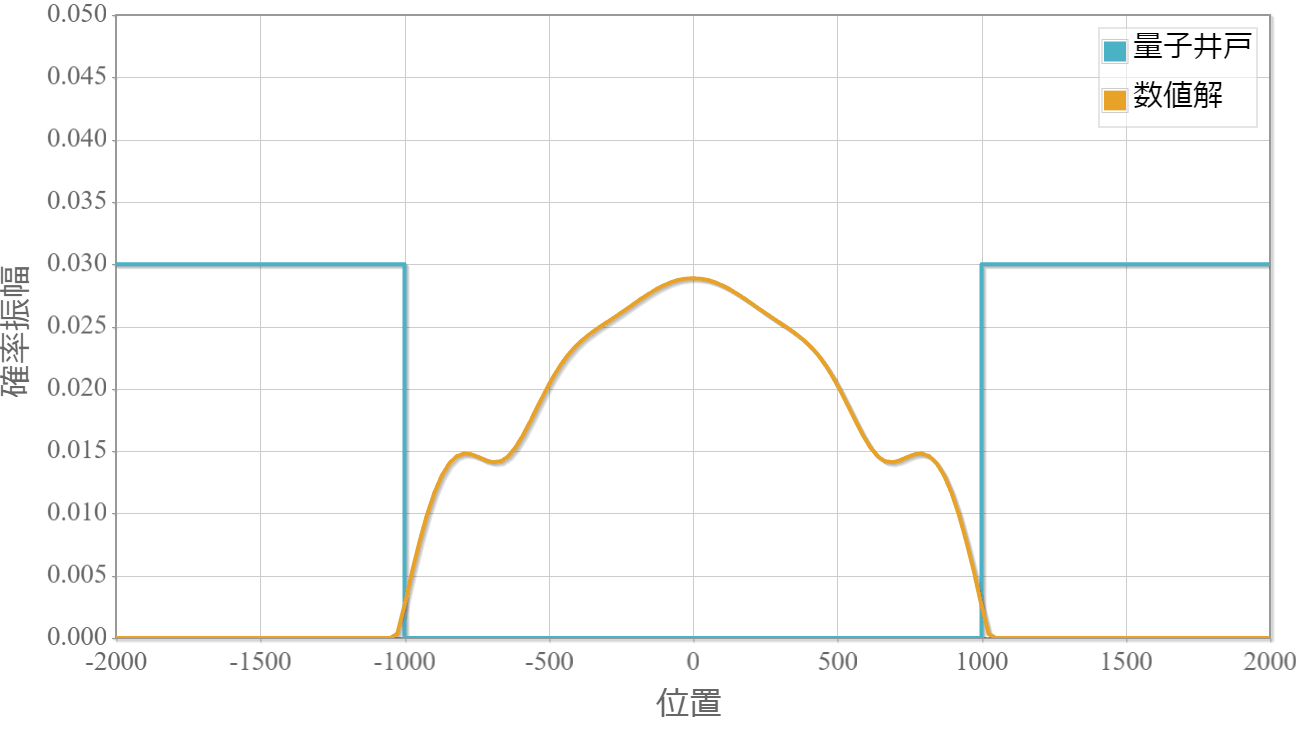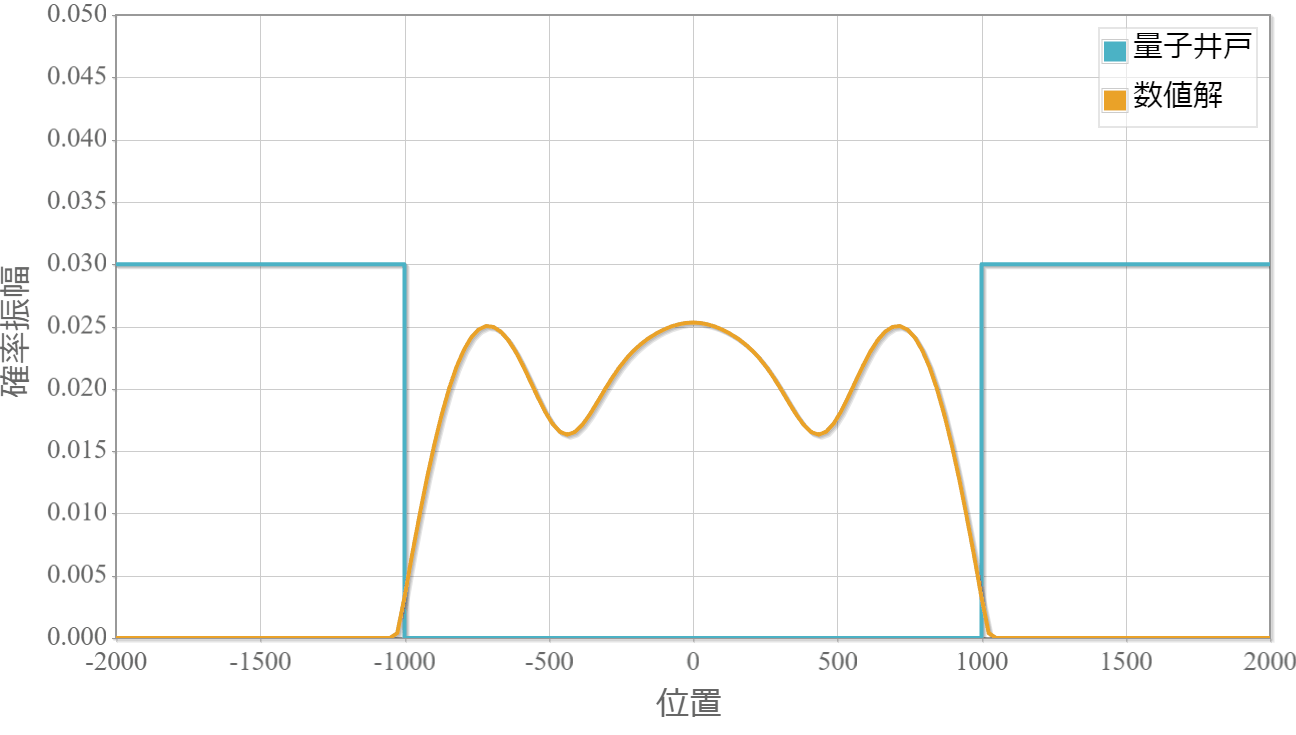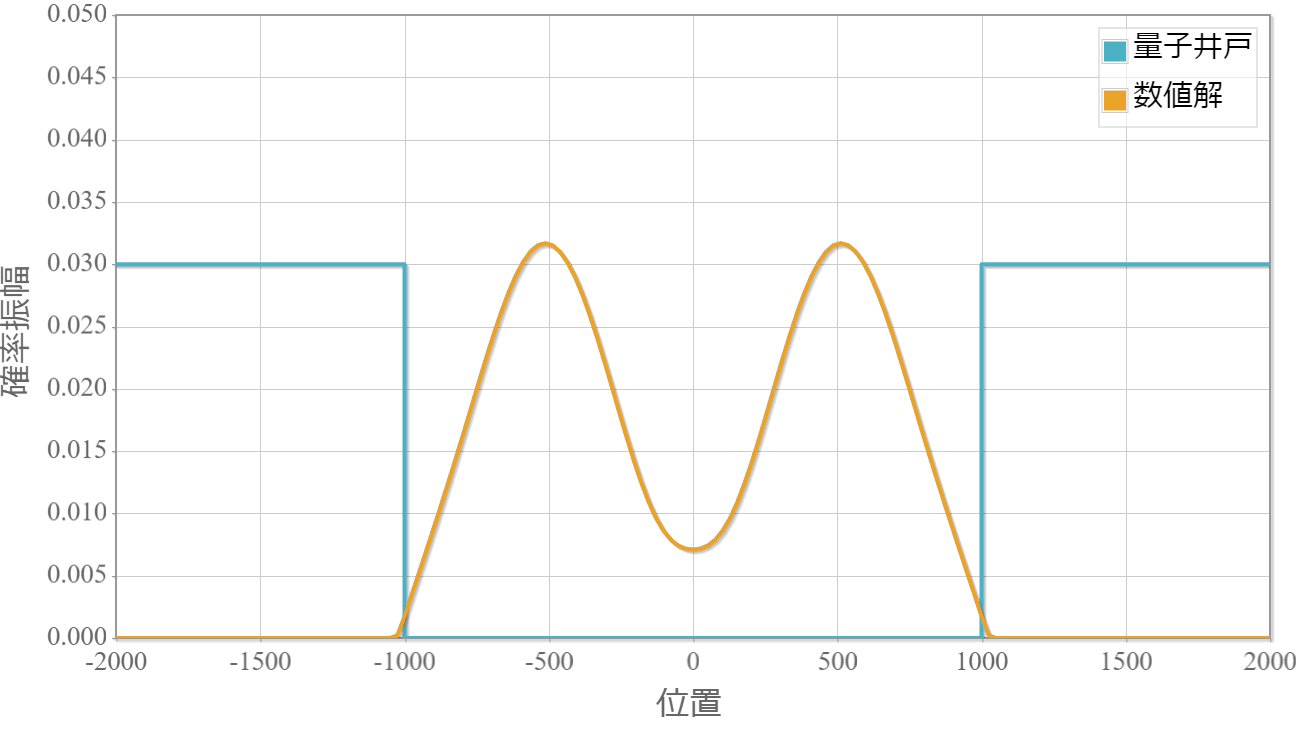
時間スケール：4E-14[s]（１コマ）
空間スケール：1E-11[m]
波束を生成する平面波の項数：500
フーリエ級数展開係数の項数：2048
ルンゲ・クッタの時間刻み幅：1.0E-16[s]
今後の計算予定（メモ）
・浅い量子井戸の場合
・２重量子井戸の場合
・ポテンシャルが時間依存する場合
プログラムソース（C++）
・http://www.natural-science.or.jp/files/physics/QuantumPhysics_OpenMP12.cpp
※VisualC++、GCC（MinGW）で動作確認しています。
