【量子力学再入門13】
浅い井戸型ポテンシャル中の波束の運動（スペクトル法）
文責：遠藤 理平 （2018年5月23日）
カテゴリ：仮想物理実験室(325)
前回はスペクトル法を用いた例として、深い井戸型ポテンシャル中の波束の運動を数値計算してみました。
本稿では、井戸の深さが浅くて、波束を構成するエネルギーの２０％程度が井戸の高さより高い場合です。
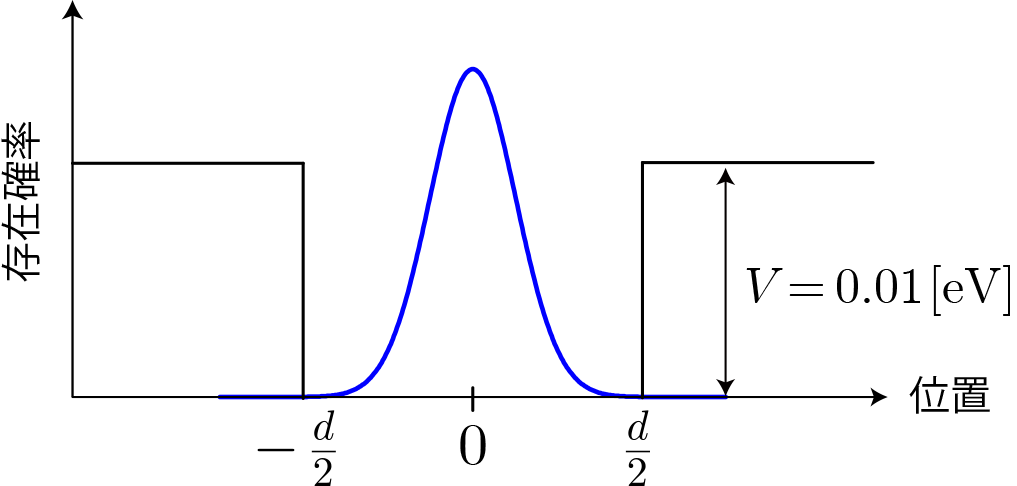
ポテンシャル項のフーリエ級数展開
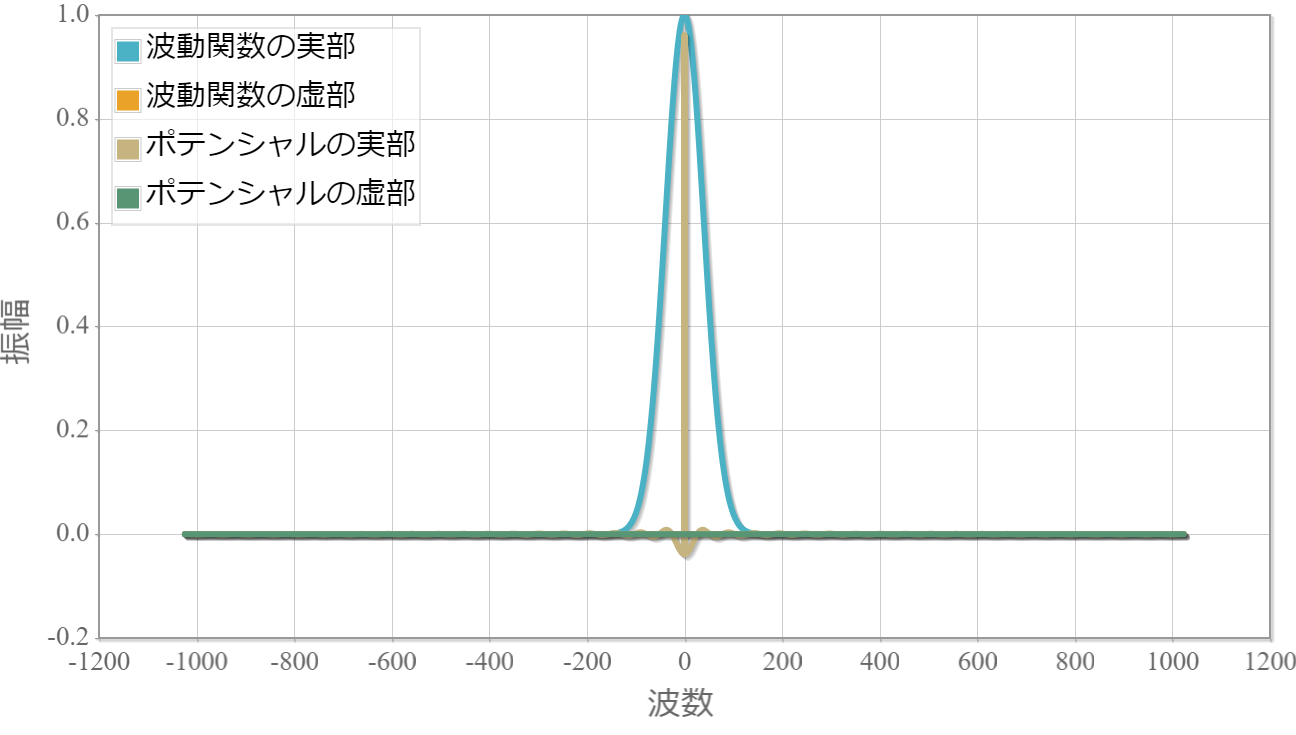
次の図は、幅2000E-11[m]、高さ5.0eVの井戸型ポテンシャルと、波動関数の初期状態のフーリエ級数展開の展開係数です。横軸が波数に対応し、縦軸が展開係数です。高さはそれぞれ適当にスケールさせています。幅の広い井戸型ポテンシャルの場合、フーリエ級数展開の収束が思いのほか早いです。
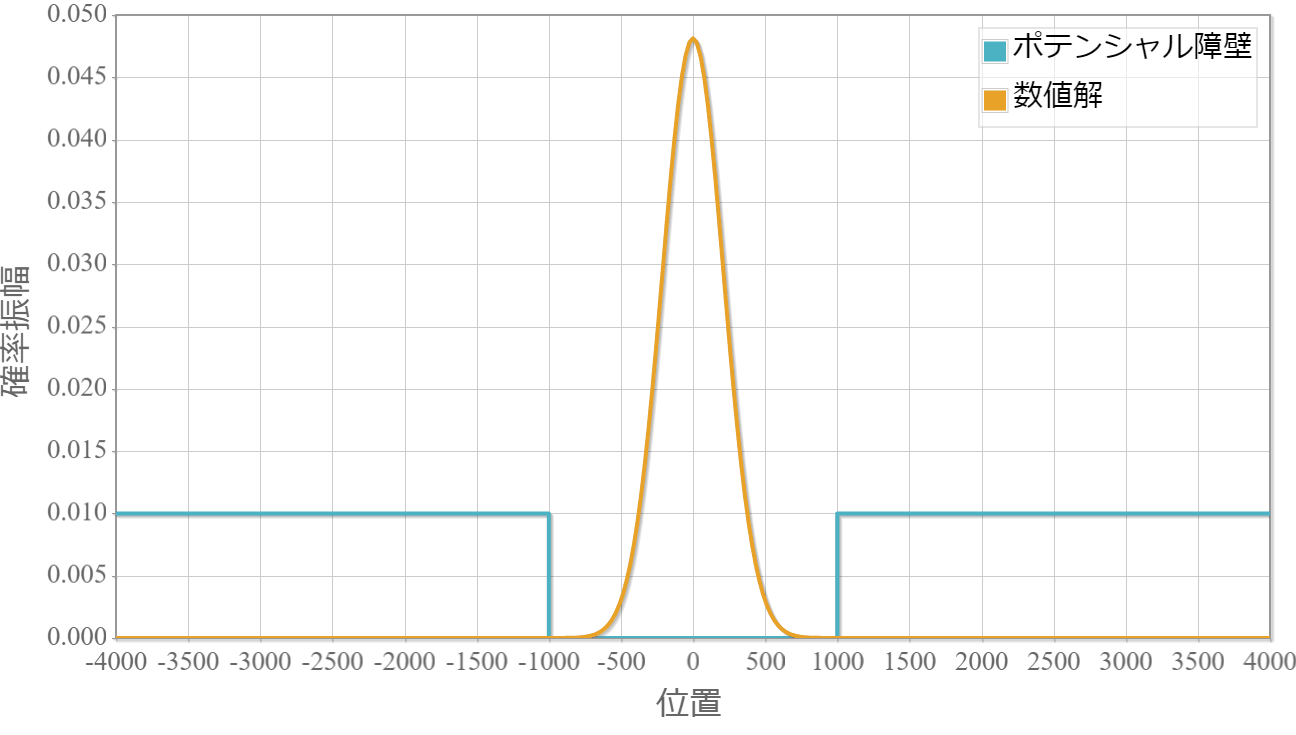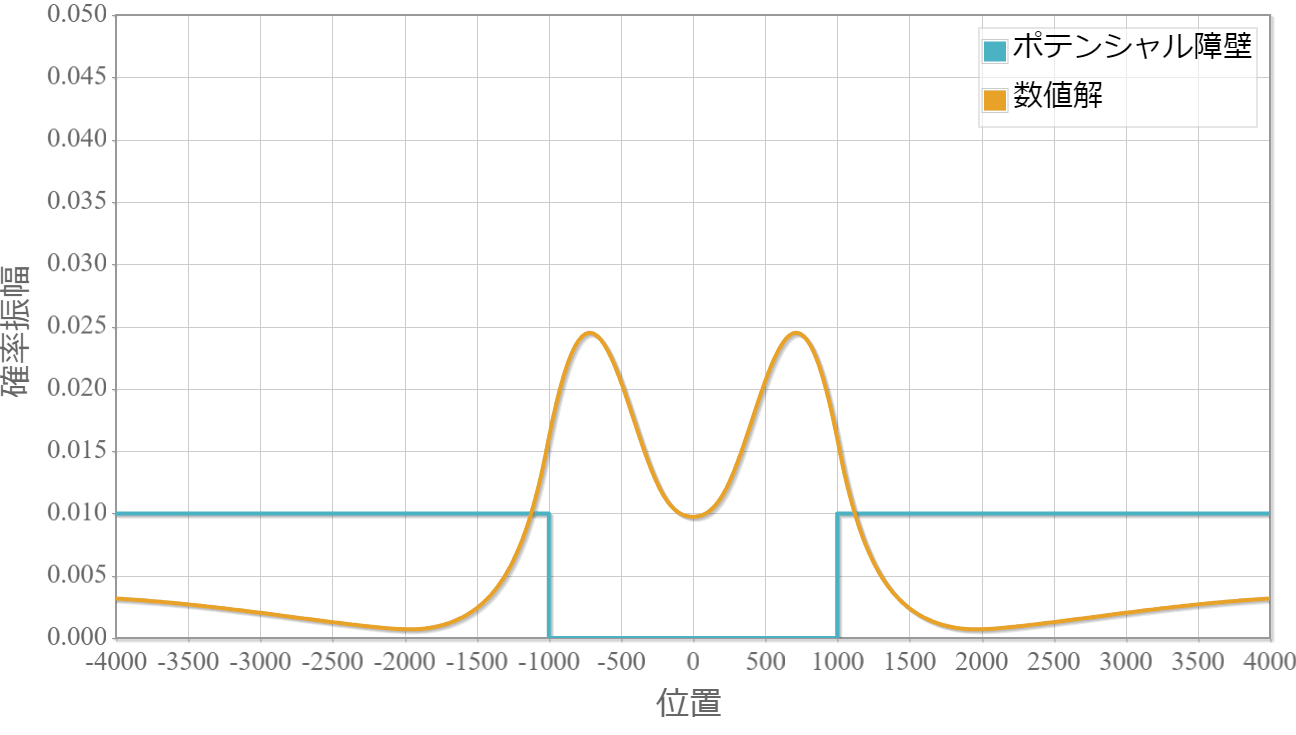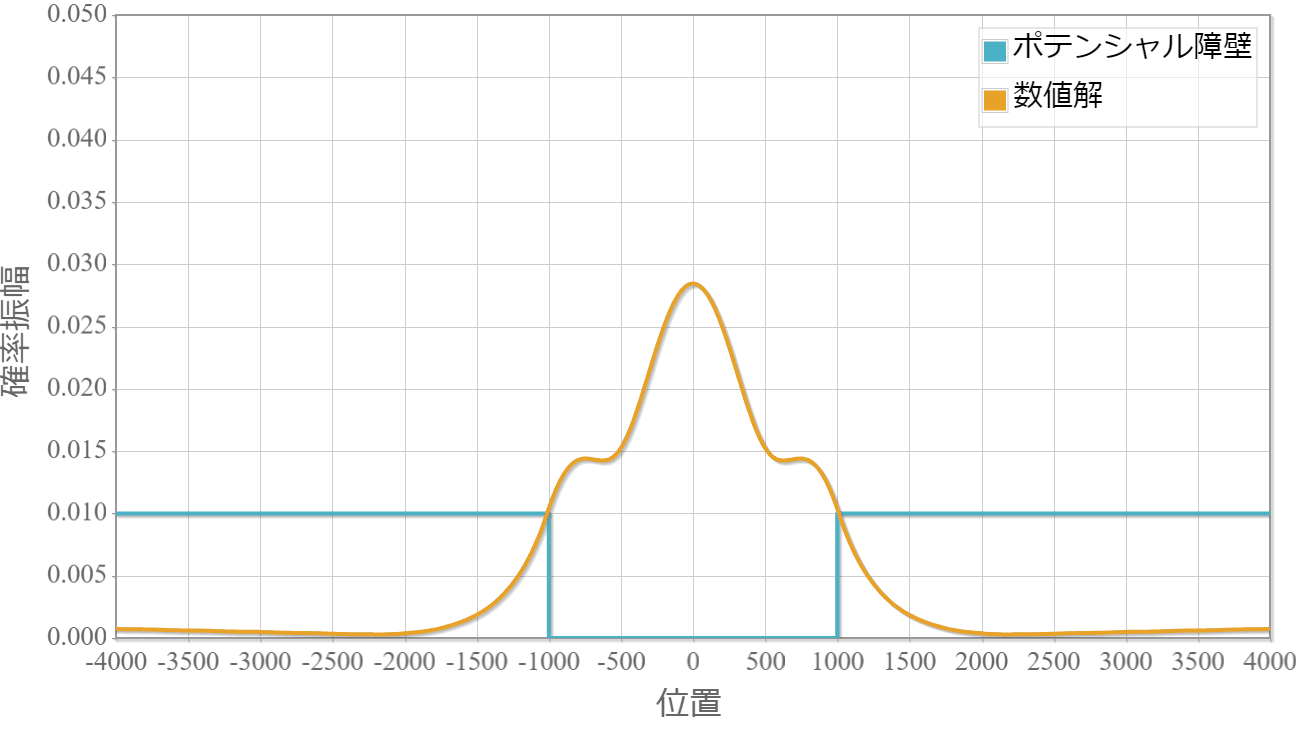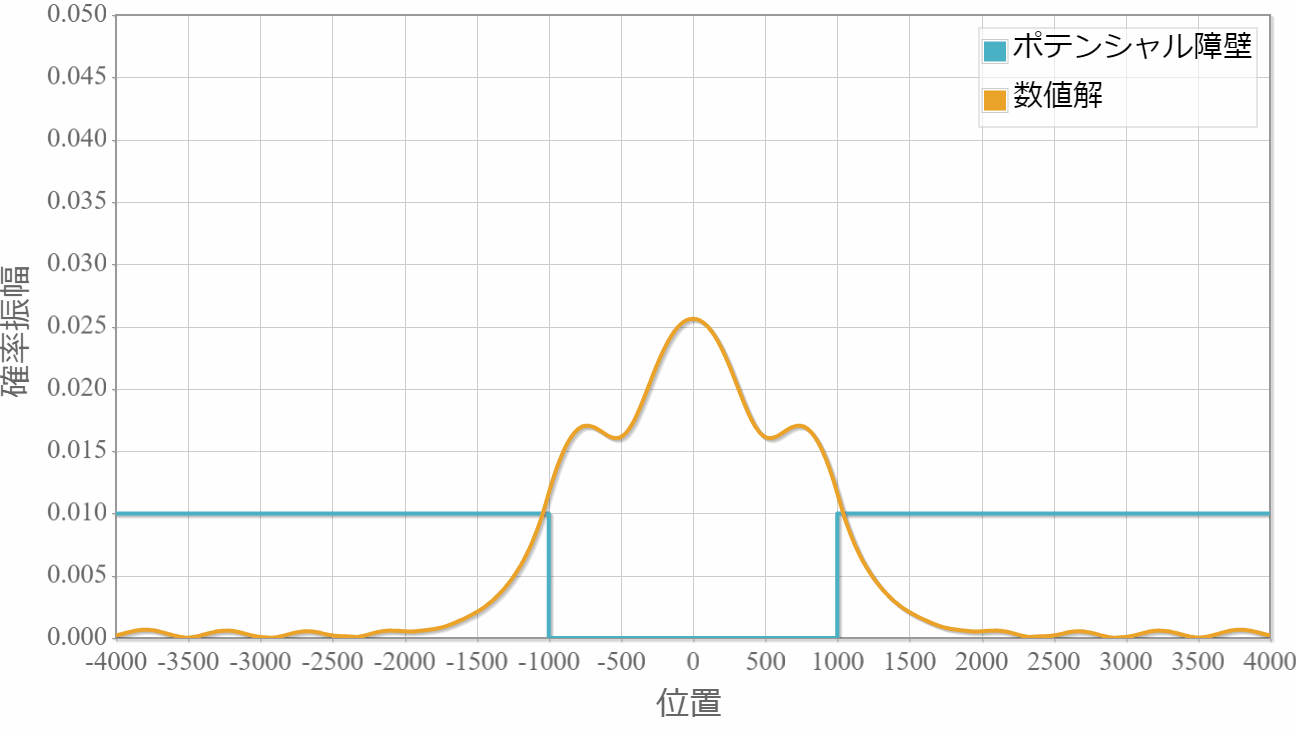
時間発展の計算結果
波束を構成するエネルギーの一部が外部に染み出した後は、残ったエネルギーで構成された波束が周期的な運動を行っている様子がわかります。
時間スケール：4E-14[s]（１コマ）
空間スケール：1E-11[m]
波束を生成する平面波の項数：500
フーリエ級数展開係数の項数：2048
ルンゲ・クッタの時間刻み幅：1.0E-16[s]
今後の計算予定（メモ）
・２重量子井戸の場合
・ポテンシャルが時間依存する場合
・ポテンシャルが複素数の場合
プログラムソース（C++）
・http://www.natural-science.or.jp/files/physics/QuantumPhysics_OpenMP13.cpp
※VisualC++、GCC（MinGW）で動作確認しています。
