【ルンゲ・クッタで行こう！】
単振子強制振動運動シミュレーション
当方、最近の興味は物理シミュレーションとニューラルネットワークを組み合わせたある種の最適化問題を解くことを目的としています。その準備として、簡単な物理系の数値計算の動作チェックを行います。
単振子強制振動運動とは
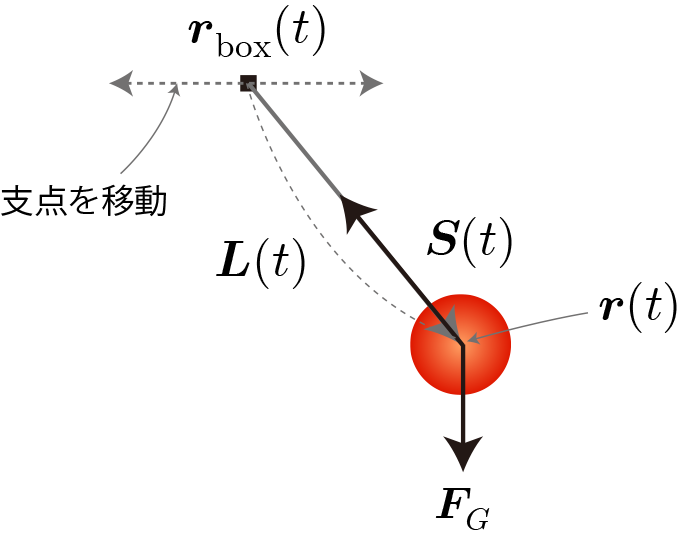
単振子とは伸び縮のしない紐に結び付けられたおもりです。本稿で扱う単振子強制振動運動は、紐に結び付けられたおもりの反対側の支点を水平に揺らすことで振動させる運動を表します。このときの支点の水平運動の振動数によっておもりの振れ角は異なり、特定の振動数のときのみ大きな振幅となります。このような現象は共鳴現象と呼ばれます。 下図は異なる振動数で強制振動運動させた際のスナップショットです。
※HTML5による単振子強制振動運動シミュレーションはこちら
単振子強制振動運動でおもりを回転させることは可能か？
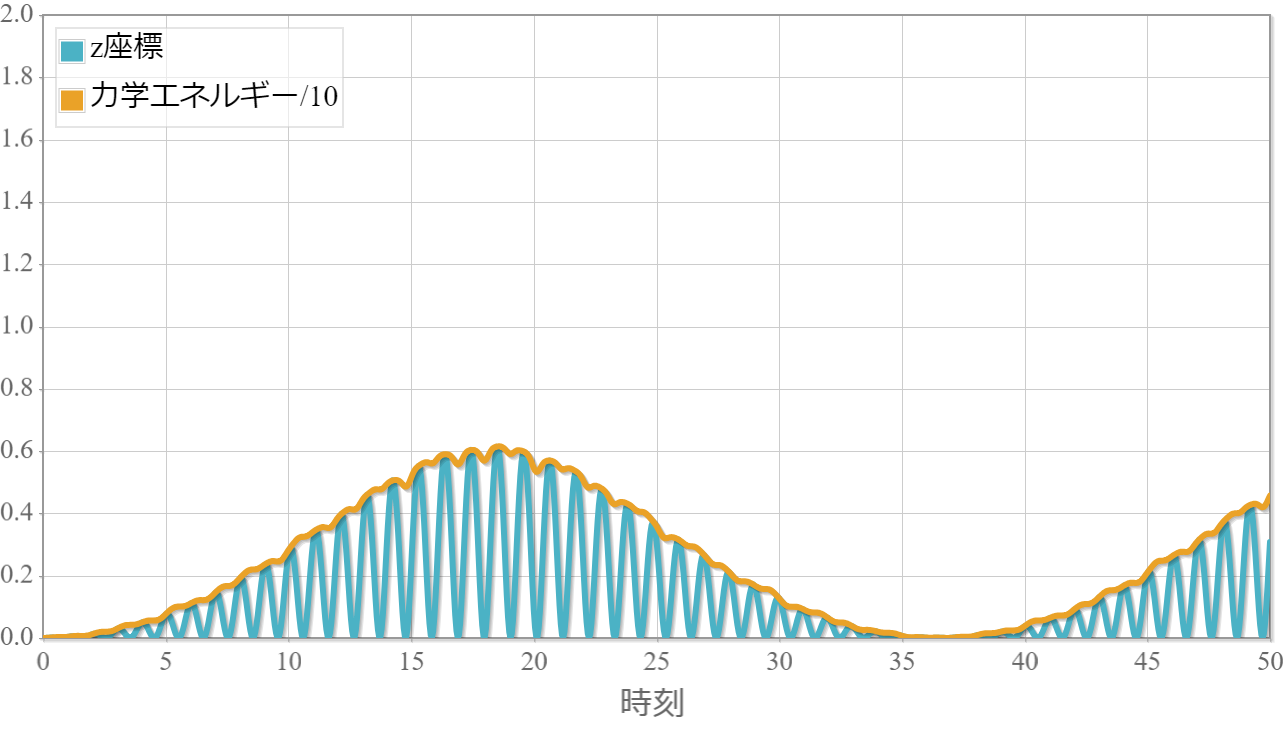
ブランコをこぐ時を思い出してください。静止状態からこぎ始める時と、ある程度振動運動が大きくなってからでは、足に力を入れる周期（振動数）が異なります。 つまり、単振子強制振動運動でも静止状態とその後の状態では共鳴角振動数が異なるため、単一の振動数ではある程度以上大きな振動運動にはなりません。 下図は、1[m]のひもに1[kg]のおもりを結びつけ、支点を静止時の共鳴角振動数で強制振動運動させた結果です（振幅は0.1[m]）。横軸が時刻、縦軸がおもりのz座標（静止状態の高さを０とします）と力学的エネルギーを１０で割った値（重力加速度を10として計算しているため、１０で割ると静止時の高さと力学的エネルギーが一致します）です。 おもりの高さが１で振り子は水平状態、２で振り子が真上となります。
考察と次の課題
・単振子強制振動運動シミュレーションは正しく計算できました。
・単振子強制振動運動で振り子が回転する支点の角振動数分布をニューラルネットワークを用いて導いてみます。
プログラムソース（C++）
・http://www.natural-science.or.jp/files/NN/ForcedVibrationSinglePendulumMotion_RK4.zip
※VisualStudio2017のソルーションファイルです。GCC（MinGW）でも動作確認しています。
参考
上記シミュレーションは、ルンゲ・クッタ法という常微分方程式を解くアルゴリズムを用いてニュートンの運動方程式を数値的に解いています。数値計算の方法などは
「ルンゲ・クッタで行こう！～物理シミュレーションを基礎から学ぶ～」を参照ください。
