【ルンゲ・クッタで行こう！】
水平自由単振子運動シミュレーション

強化学習を物理系で試すために、水平に設置されたレール上を自由に移動する滑車に伸び縮みのしないひも（棒）で取り付けられたおもりを用意します。この振り子の一般的な呼び名がわからないので、本稿では「水平自由単振子」と呼ぶことにします。この滑車には外部から自由に力を加えることができるとし、単振子を制御することができるとします。本稿では強化学習の準備として、この物理系の数値計算を行うための計算アルゴリズムを示すとともに、動作チェックを行います。

水平自由単振子運動の数理モデル

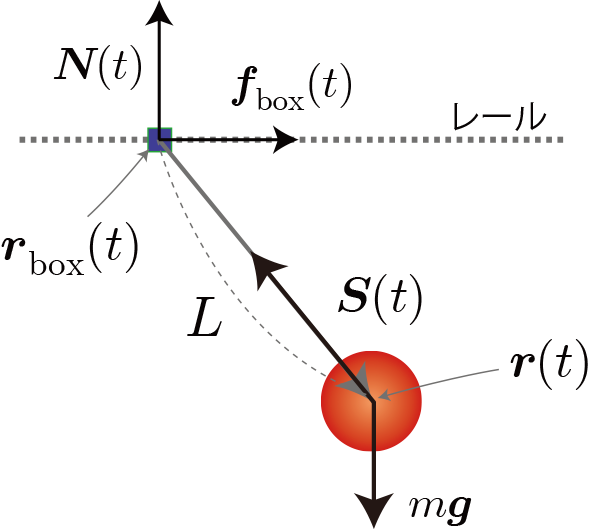
上図は滑車とおもりに加わる力を示した模式図です。滑車とおもり質量と位置ベクトルを$m_{\rm box} $, $m$、$\boldsymbol{r}_{\rm box} (t)$, $ \boldsymbol{r}(t)$、長さ$L$の伸び縮しないひもに加わる張力$\boldsymbol{S}(t)$、重力加速度ベクトルを$\boldsymbol{g}$、滑車がレールから受ける垂直抗力を$\boldsymbol{N}(t)$、滑車に与える外力を$ \boldsymbol{f}_{\rm box} $と表しています。滑車とおもりが受ける力をまとめると次のとおりです。

\begin{align} \boldsymbol{F}_{\rm box} &=m_{\rm box} \boldsymbol{g} - \boldsymbol{S} +\boldsymbol{N}_{\rm box}+ \boldsymbol{f}_{\rm box}\\ \boldsymbol{F} &= m \boldsymbol{g} + \boldsymbol{S} \end{align}

滑車はレールから外れないと仮定すると、滑車には垂直方向成分がキャンセルされる方向に垂直抗力が働くので、 垂直抗力$\boldsymbol{N}$は

\begin{align} \boldsymbol{N} =-m_{\rm box} \boldsymbol{g} + (\boldsymbol{S} \cdot \hat{\boldsymbol{z}})\hat{\boldsymbol{z}} \end{align}

と表されます。これを代入すると滑車に加わる力は次のとおりです。

\begin{align} \boldsymbol{F}_{\rm box} =- \boldsymbol{S} +(\boldsymbol{S} \cdot \hat{\boldsymbol{z}})\hat{\boldsymbol{z}}+ \boldsymbol{f}_{\rm box} \end{align}

滑車とおもりの加速度はニュートンの運動方程式から次のようになります。

【計算アルゴリズム】水平自由単振子の滑車とおもりの加速度ベクトル

\begin{align} \boldsymbol{a}_{\rm box} &=\frac{\boldsymbol{F}_{\rm box}}{m_{\rm box}} = \frac{1}{m_{\rm box}} \left[ - \boldsymbol{S} +(\boldsymbol{S} \cdot \hat{\boldsymbol{z}})\hat{\boldsymbol{z}}+ \boldsymbol{f}_{\rm box} \right]\\ \boldsymbol{a} &=\frac{\boldsymbol{F}}{m} = \boldsymbol{g} + \frac{\boldsymbol{S}}{m} \end{align}

あとはこれを用いてルンゲ・クッタ法などの常微分方程式を数値解法を用いて計算すれば良さそうですが、まだ$\boldsymbol{S}$は未定です。この$\boldsymbol{S}$を決定するには「伸び縮みのしないひも」に接続されているという拘束条件を与える必要があります。

拘束条件（位置・速度・加速度）

拘束条件と言っても難しくはありません。ひもの長さが一定というだけです。

\begin{align} |\boldsymbol{r}-\boldsymbol{r}_{\rm box}| = L \end{align}

これは位置に関する拘束条件を意味します。さらに両辺を２乗して、時間で微分すると

\begin{align} (\boldsymbol{r}-\boldsymbol{r}_{\rm box}) \cdot (\boldsymbol{v}-\boldsymbol{v}_{\rm box}) = 0 \end{align}

が得られ、これは速度に関する拘束条件です。相対位置ベクトルと相対速度ベクトルは直交することを表しています。さらに上式を時間で微分すると

\begin{align} (\boldsymbol{r}-\boldsymbol{r}_{\rm box}) \cdot (\boldsymbol{a}-\boldsymbol{a}_{\rm box}) + |\boldsymbol{v}-\boldsymbol{v}_{\rm box}|^2 =0 \end{align}

となり、これは加速度に関する拘束条件となります。これらの拘束条件とニュートンの運動方程式から得られた加速度ベクトルから、$\boldsymbol{S}$は次のとおりになります。

【計算アルゴリズム】水平自由単振子の滑車－おもり間の張力ベクトル

\begin{align} \boldsymbol{S} = \frac{1}{ \frac{ ( \boldsymbol{L}\cdot \hat{\boldsymbol{z}})^2}{m_{\rm box}}- \frac{m+m_{\rm box}}{mm_{\rm box}}L^2 } \left[ |\boldsymbol{v}-\boldsymbol{v}_{\rm box}|^2+\boldsymbol{g}\cdot \boldsymbol{L} - \frac{\boldsymbol{f}_{\rm box}\cdot\boldsymbol{L}}{m_{\rm box}} \right] \boldsymbol{L} \end{align}

ただし、$\boldsymbol{L} \equiv \boldsymbol{r}-\boldsymbol{r}_{\rm box}$ です。

計算結果

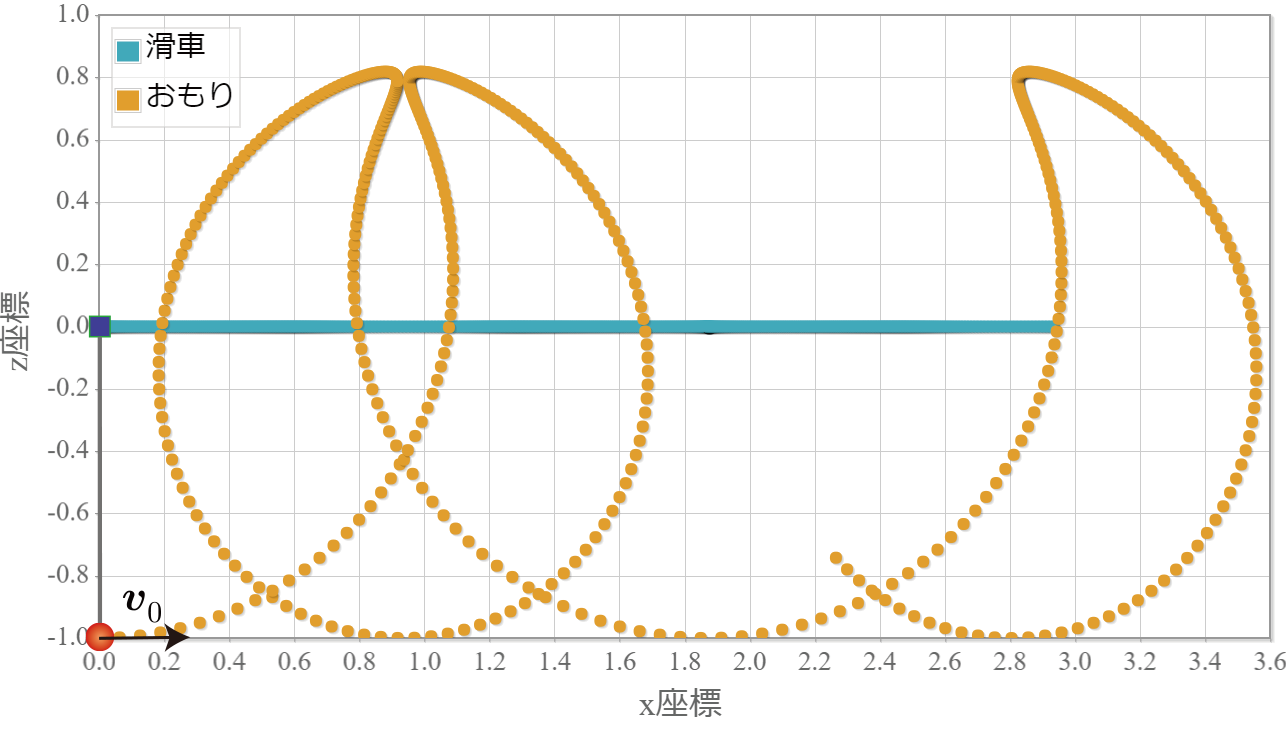
滑車とおもりの質量をそれぞれ$ m_{\rm box}=10$、$m=1$、ひもの長さ$L=1$、重力加速度ベクトル$\boldsymbol{g}=(0,0,-10)$として、上記の計算アルゴリズムを用いて２つの状態を計算してみます。１つ目はフリー滑車（初速度０、外力０）でおもりに初速度を与えた場合です。初速度の大きさは滑車が固定されている場合（実質的に通常の単振子）におもりがちょうど真上に来る$v_0=\sqrt{2mgL}$を与えます。下図は滑車とおもりの軌跡（５秒間）です。初期条件としておもりに与えられたエネルギーのうち、おおよそ１０％が滑車の運動エネルギーに変換され、おもりは頂点まで来ることができていない様子がわかります。なお、滑車とおもりの相対位置のみを考えると、周期的なうんどうとなります。

図（１）フリー滑車に初速度を与えたおもりの軌跡（５秒間）

２つ目は反対に、初期条件としておもりを静止させておいて、滑車に周期的な力

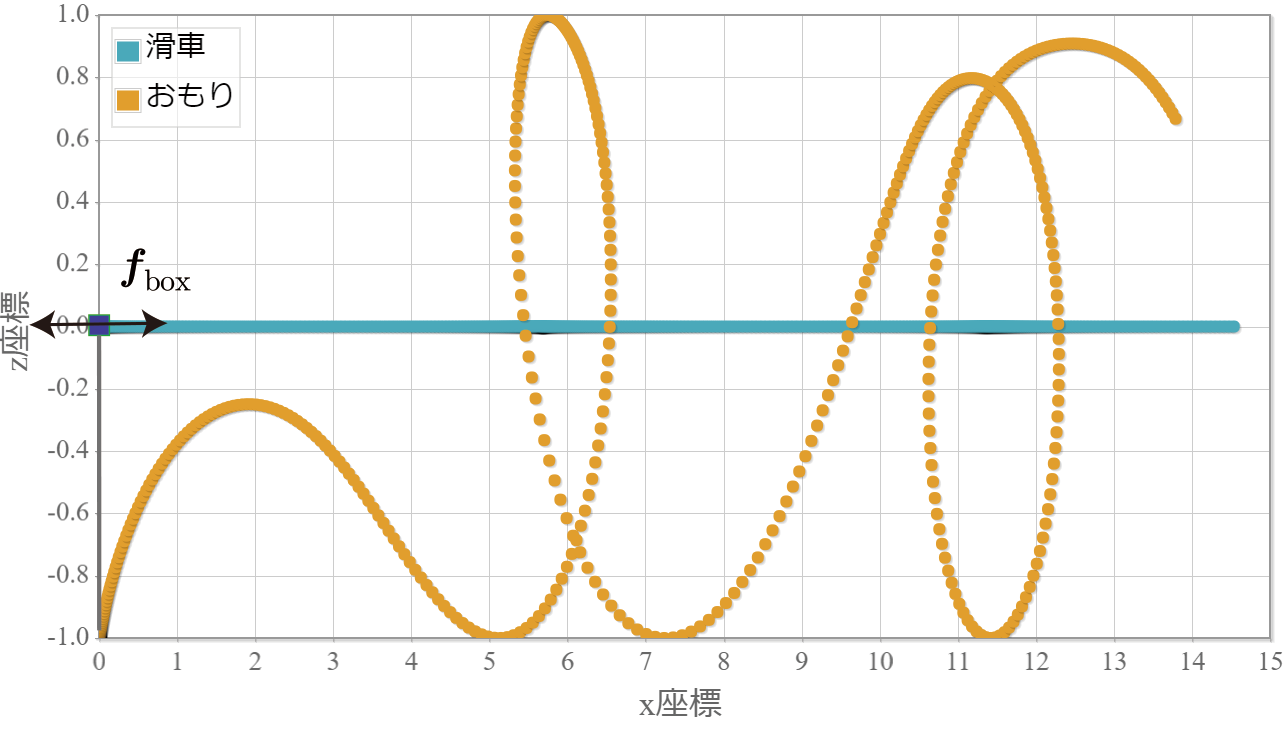
\begin{align} \boldsymbol{f}_{\rm box} = f_0\sin(\omega_{\rm box} t) \hat{\boldsymbol{x}} \end{align}

を与えます。$\omega$は振動の速さを表す角振動数で、微小振動時の共鳴角振動数$\omega=\sqrt{L/g}$を与えるとします。$f_0$は力の大きさで、今回は滑車に加速度$10[{\rm m/s^2}]$を与えるために$f_0=10m_{\rm box}$としています。下図は滑車とおもりの軌跡（５秒間）です。滑車は自由に動くことができるので強制振り子とは異なり、力がたとえ周期的であっても滑車は時間とともに動きます。一方、おもりは滑車から受ける力でエネルギーが供給されて、振動が大きくなって一回転している様子がわかります。

図（２）滑車に周期的な力を加えた際のおもりの軌跡（５秒間）

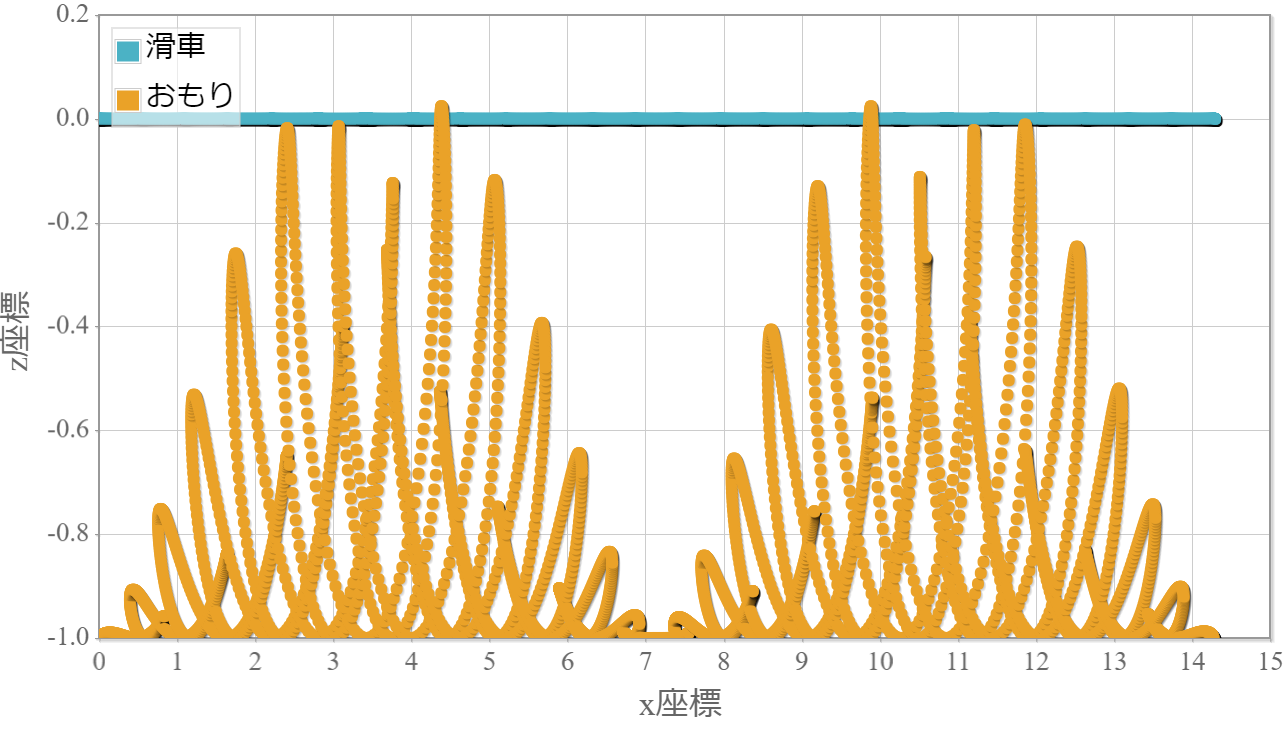
なお、周期的な力が弱い場合にはおもりは一回転しません。下図は$f_0=1m_{\rm box}$の場合です。

図（３）滑車に周期的な力（１／１０）を加えた際のおもりの軌跡（５０秒間）

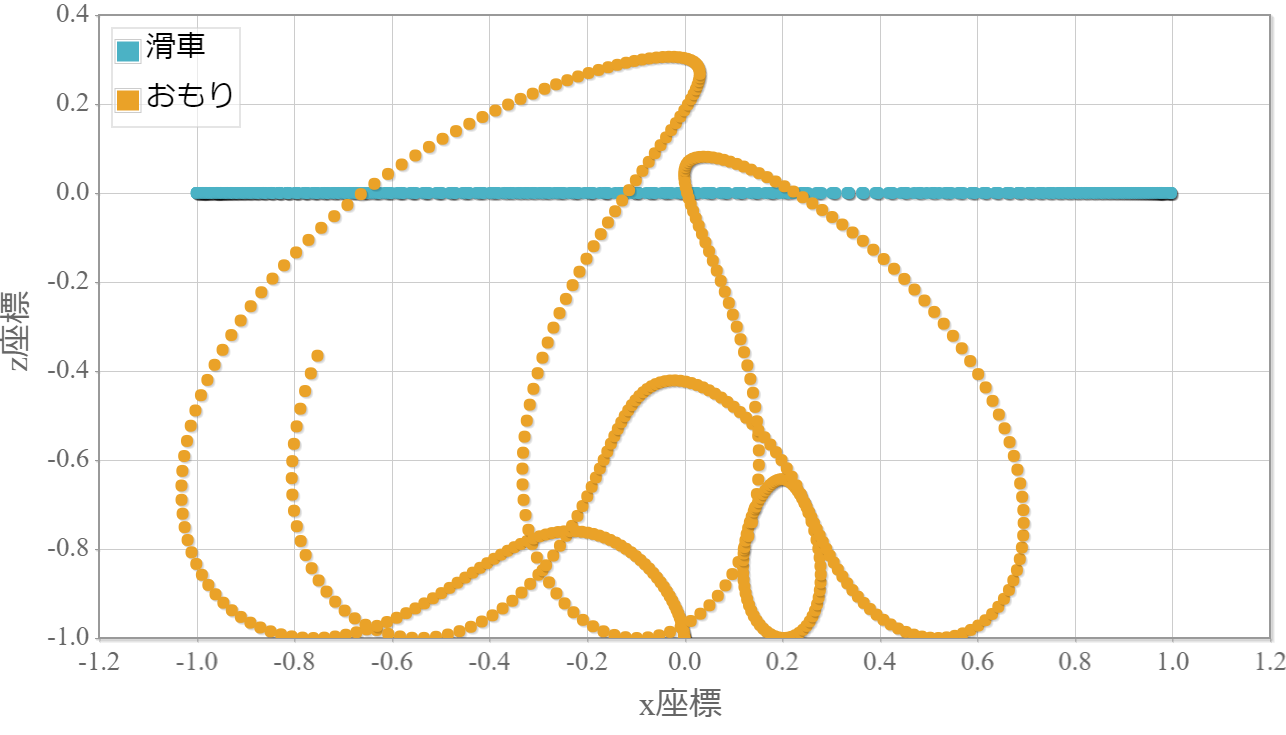
ちなみに、もし滑車の中心位置を原点にとどめておきたければ、滑車に初速度を与える必要があります。具体的な初速度の大きさは$\boldsymbol{v}_{\rm box}(0) = -10/\omega_{\rm box}$となります。下図はその結果です。

図（４）滑車に初速度と周期的な力を加えた際のおもりの軌跡（５秒間）

考察と次の課題

・水平自由単振子運動シミュレーションは正しく計算できました。
・強化学習を用いて倒立振子などのシミュレーションを行います。

プログラムソース（C++）

・http://www.natural-science.or.jp/files/NN/HorizontalFreePendulum_RK4_Nbody.zip
※VisualStudio2017のソルーションファイルです。GCC（MinGW）でも動作確認しています。

参考

上記シミュレーションは、ルンゲ・クッタ法という常微分方程式を解くアルゴリズムを用いてニュートンの運動方程式を数値的に解いています。本稿で紹介した物理シミュレーションの方法を詳しく解説している書籍です。もしよろしければ「ルンゲ・クッタで行こう！～物理シミュレーションを基礎から学ぶ～（目次）」を参照ください。