【量子力学再入門18】
量子２重井戸中の波束の運動（スペクトル法）

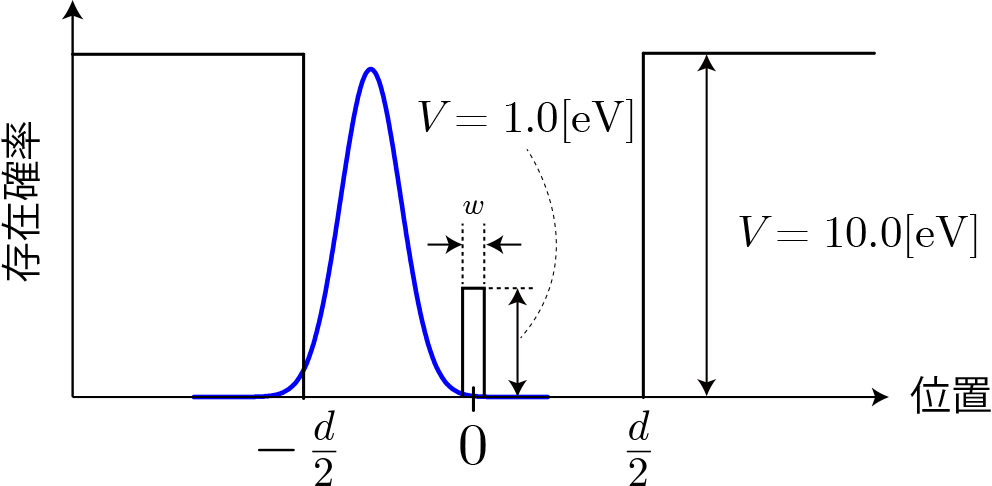
次の図のような２重井戸中の波束の運動をシミュレーションします。 ※数値計算法のスペクトル法についてはこちらを参照ください

\begin{align} V(t) =\cases{ 10 [{\rm eV}] & x < -d/2 \cr 0 [{\rm eV}] & -d/2 < x < -w/2 \cr 1.0 [{\rm eV}] & -w/2 < x < w/2 \cr 0 [{\rm eV}] & w/2 < x < d/2 \cr 10 [{\rm eV}] & d/2 < x } \end{align}

シミュレーション結果

両側のポテンシャルの高さ$10[{\rm eV}]$、中間のポテンシャルの高さ$10[{\rm eV}]$の量子２重井戸の片方に、中心エネルギー$0[{\rm eV}]$の波束（構成する平面波のエネルギーは$1[{\rm eV}]$未満）の運動をシミュレーションします。 次の計算結果は中間のポテンシャルの幅が$500\times 10^{-11}[{\rm m}]$、$100\times 10^{-11}[{\rm m}]$、$20\times 10^{-11}[{\rm m}]$の場合です。

時間スケール：2E-14[s]（１コマ）
空間スケール：1E-11[m]
波束を生成する平面波の項数：500
フーリエ級数展開係数の項数：2048
ルンゲ・クッタの時間刻み幅：5.0E-17[s]

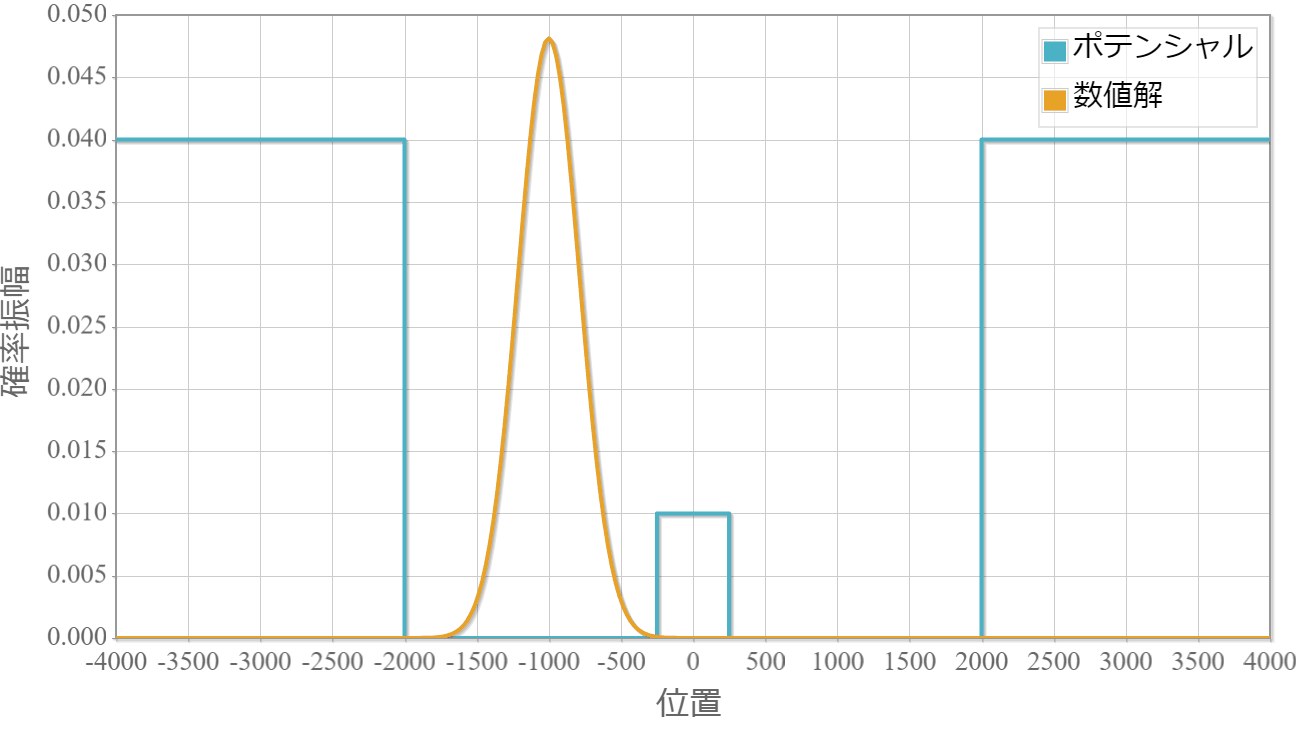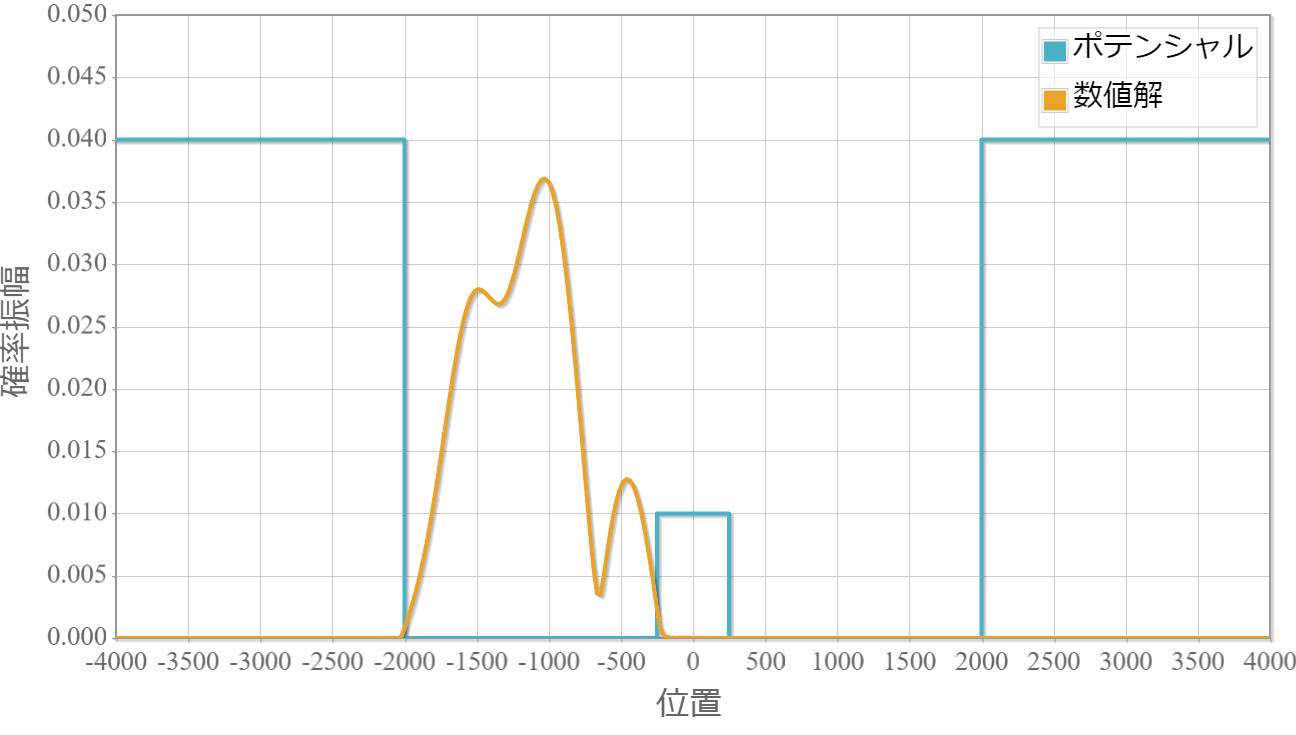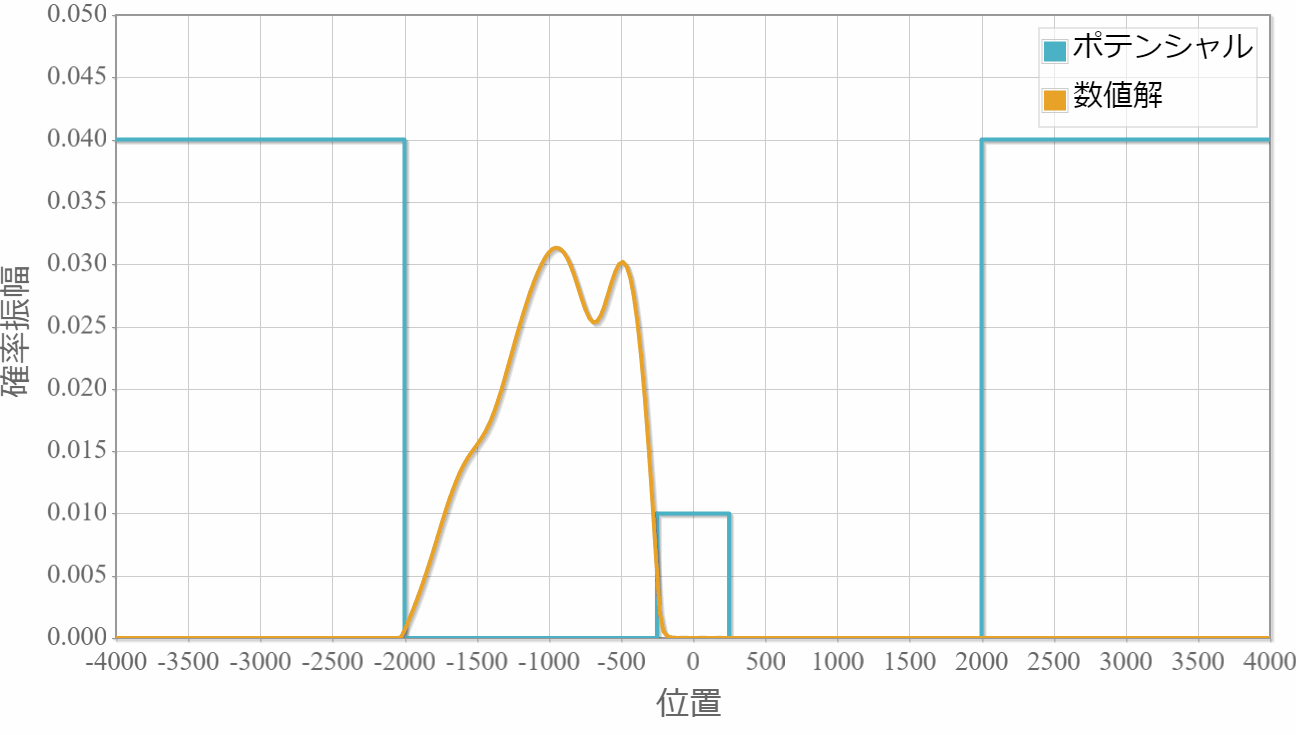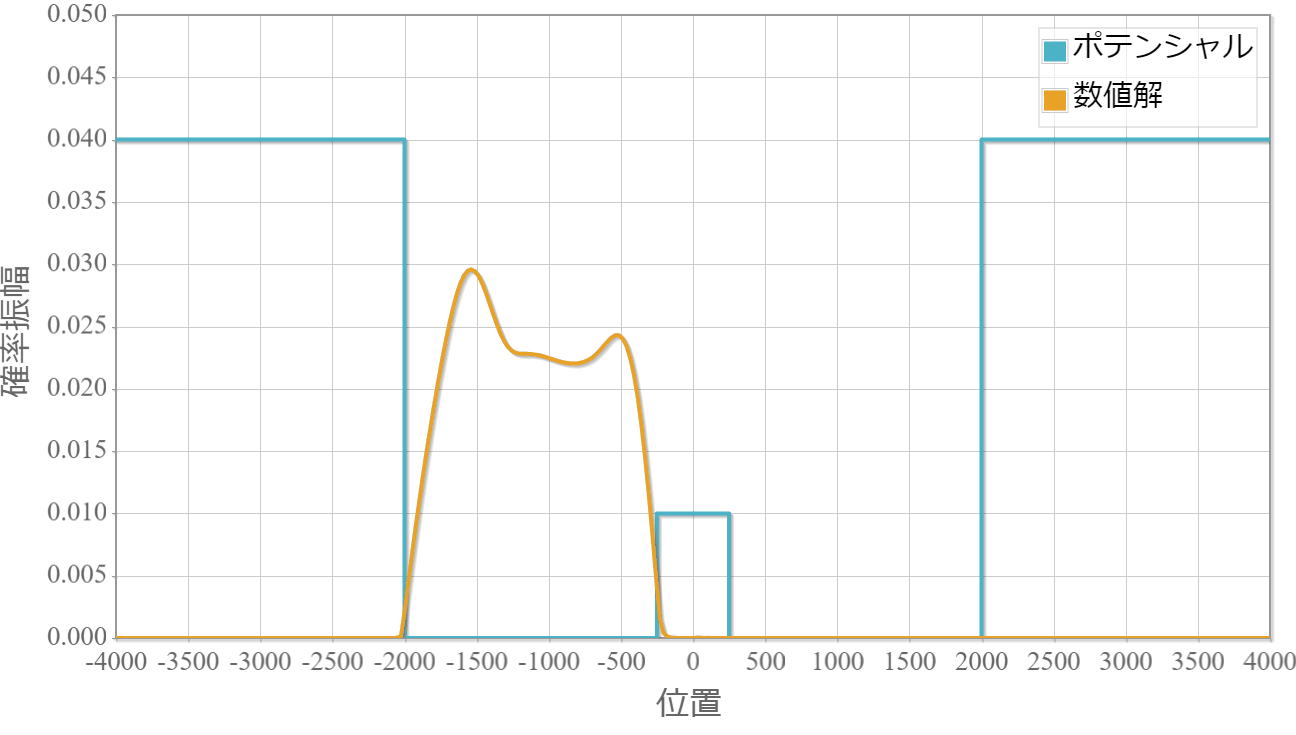
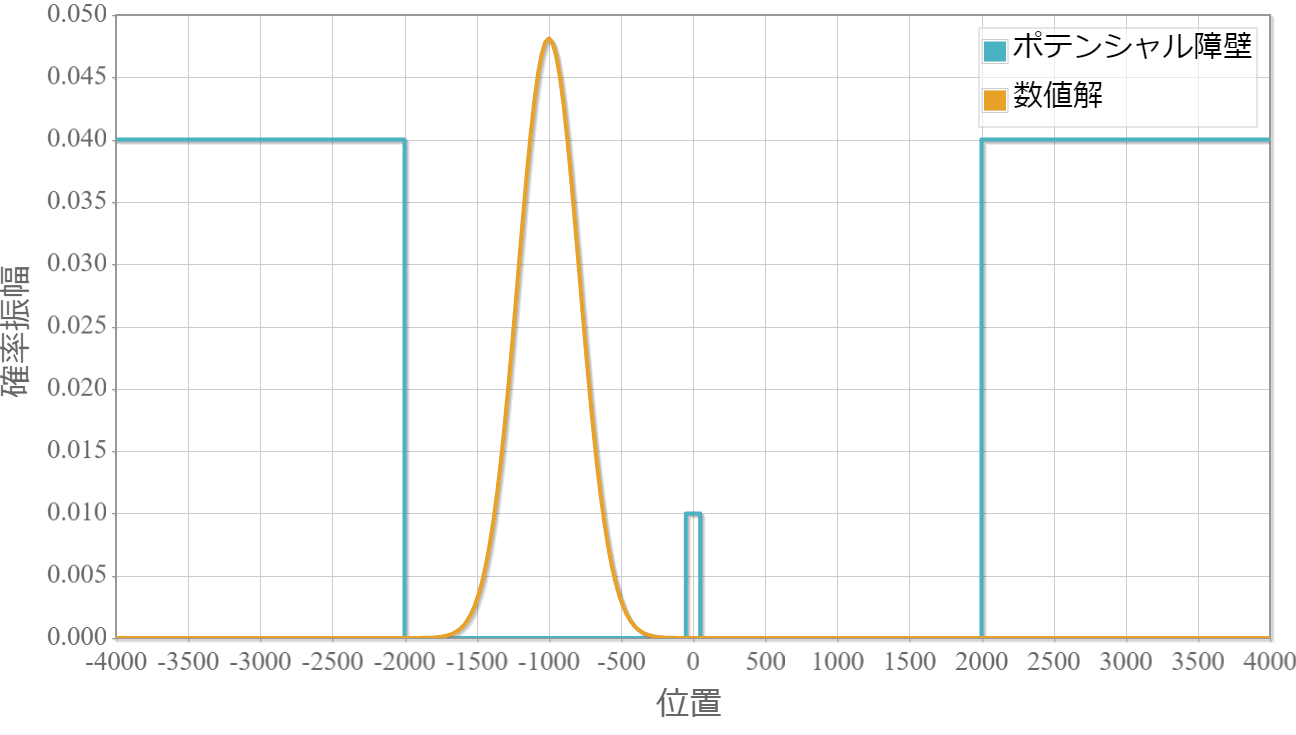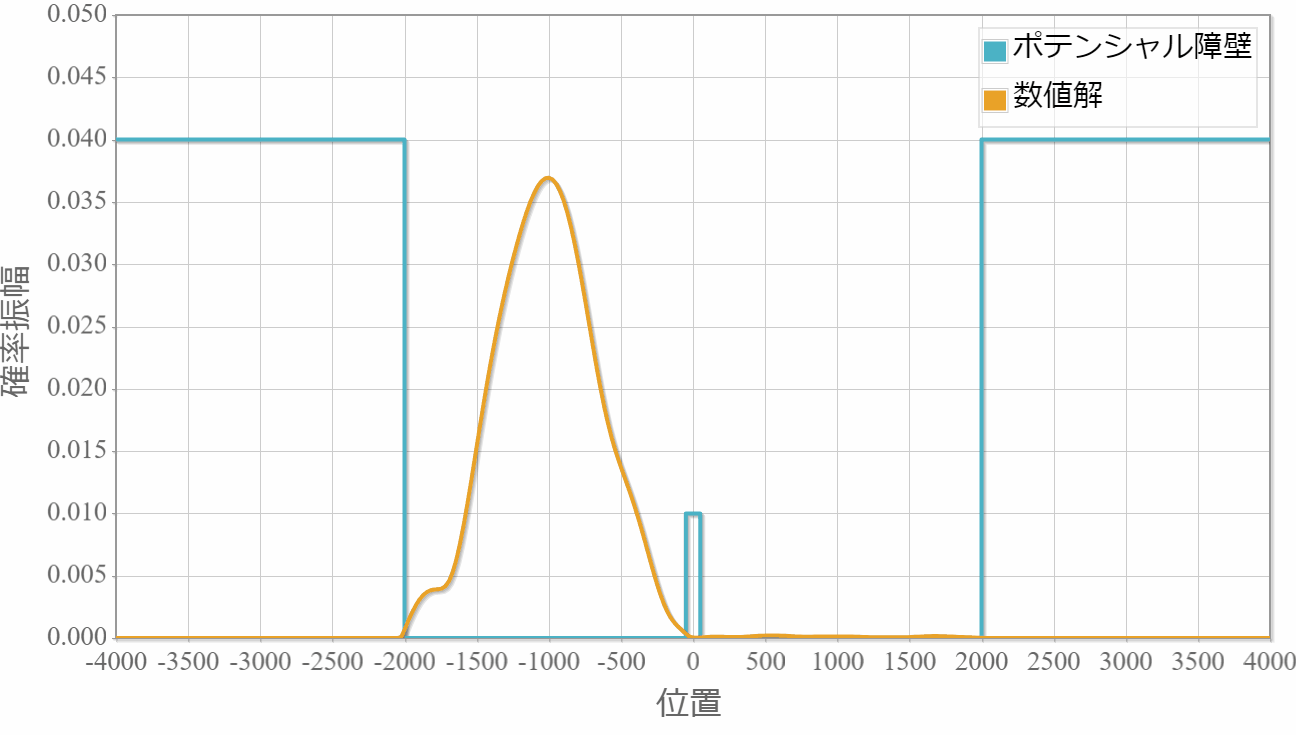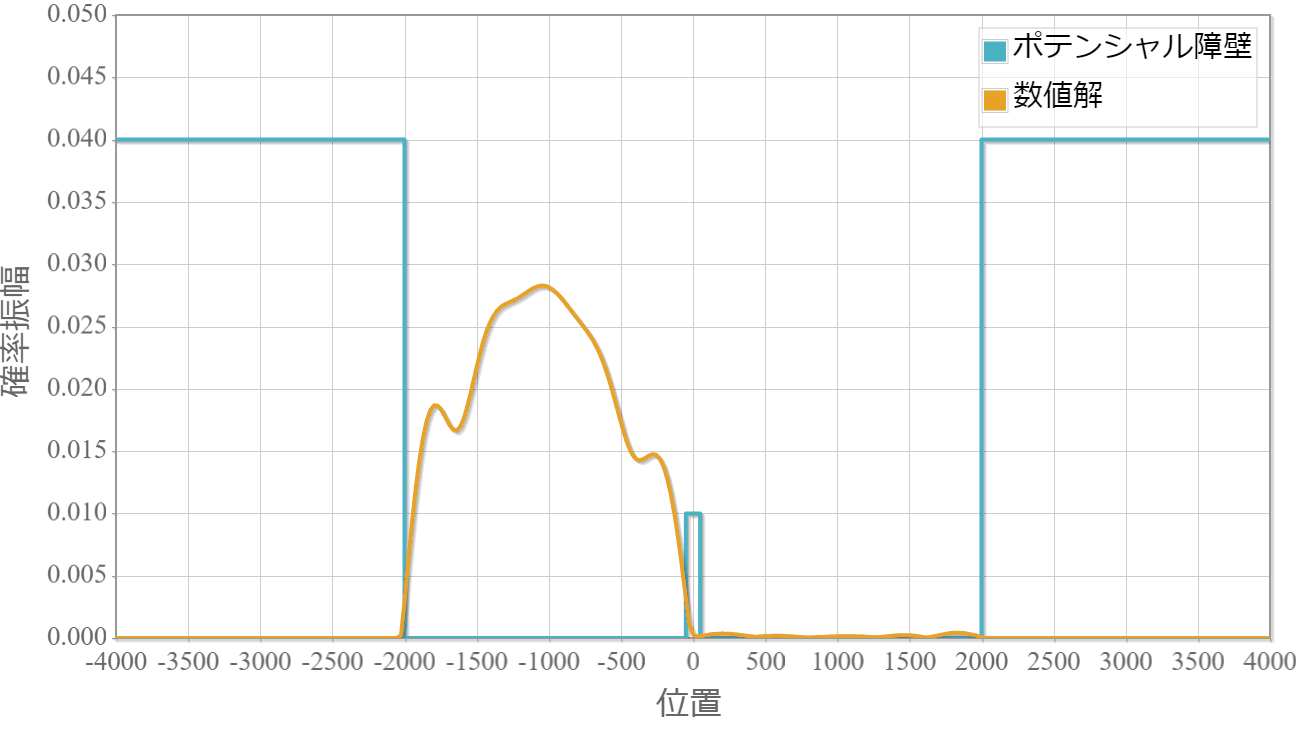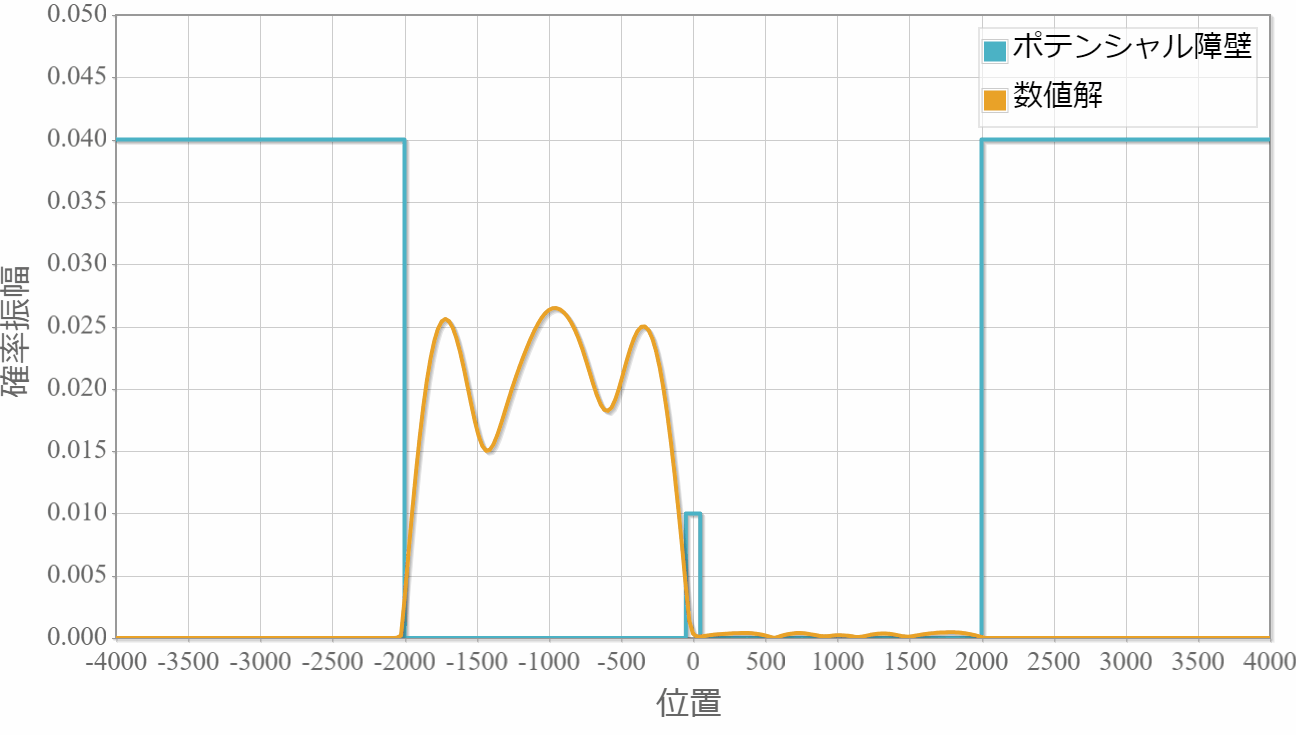
ポテンシャルの幅：$500\times 10^{-11}[{\rm m}]$

ポテンシャルの幅：$100\times 10^{-11}[{\rm m}]$

ポテンシャルの幅：$20\times 10^{-11}[{\rm m}]$

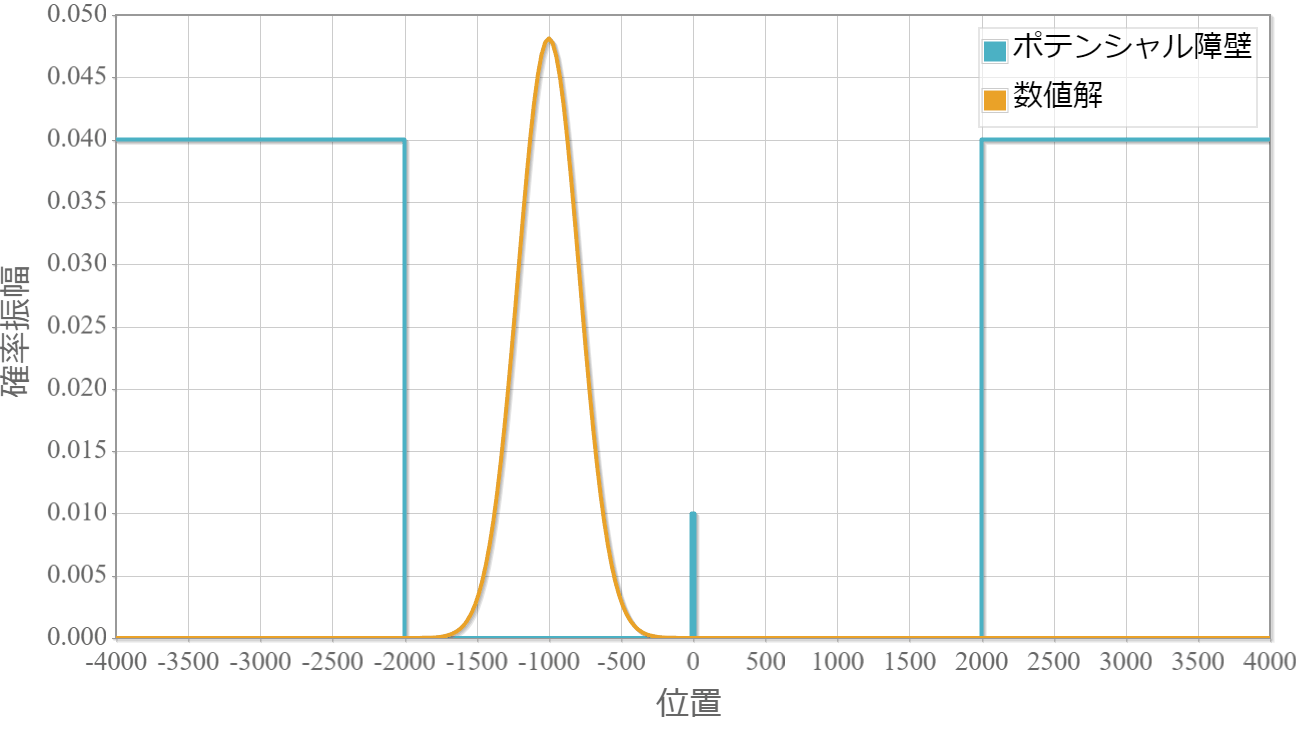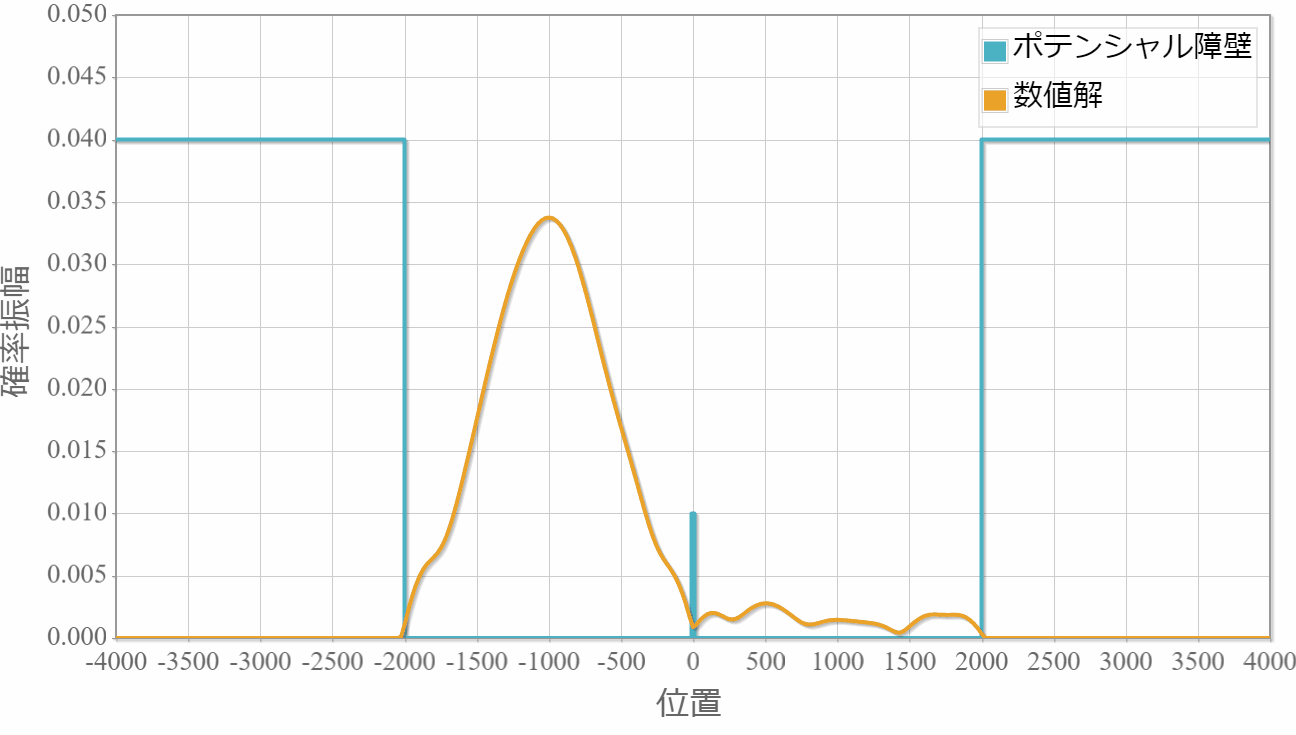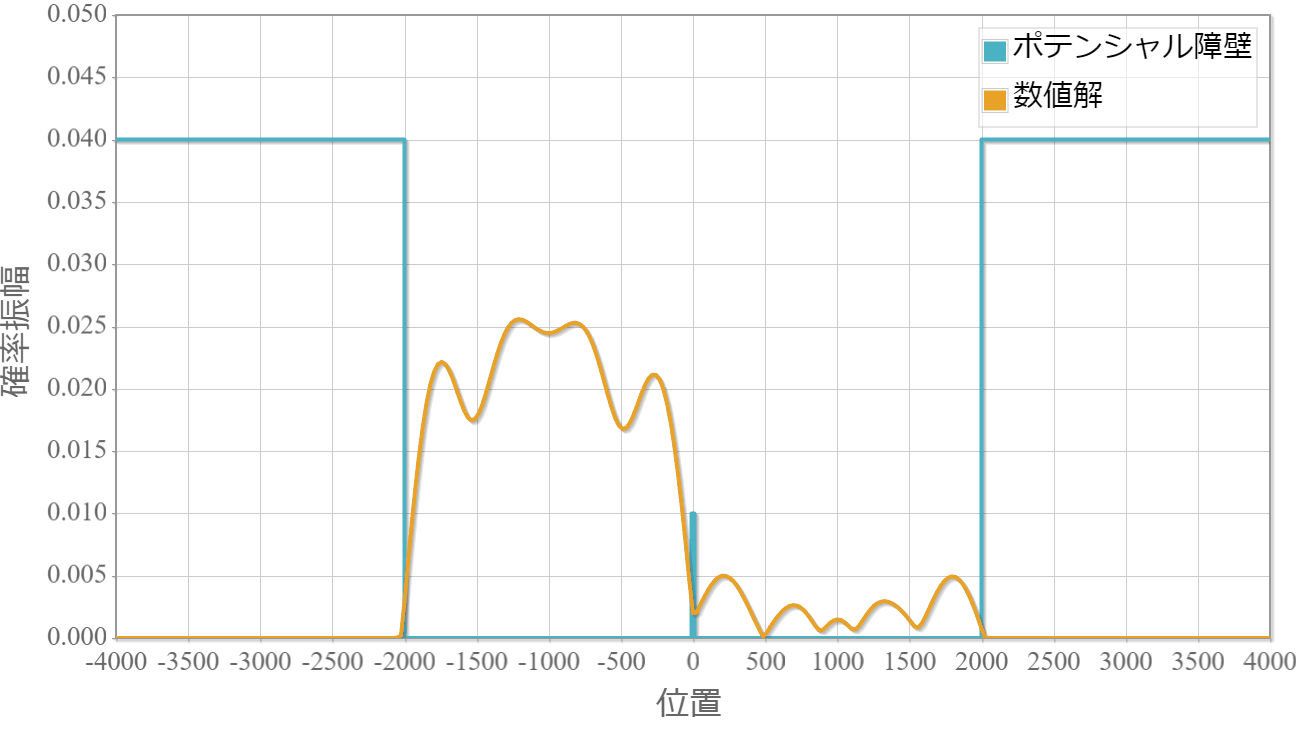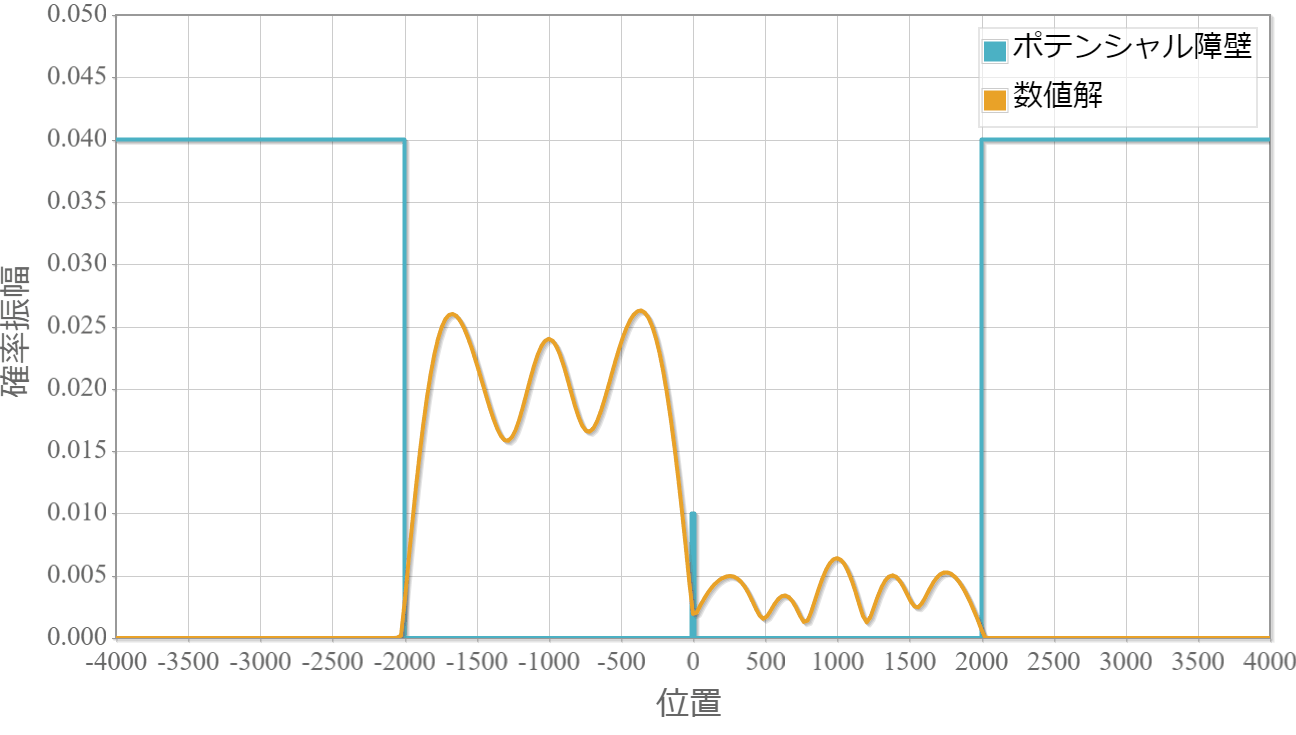
薄いほどトンネル効果で障壁を透過して反対側に滲み出ていく様子が確認できました。

今後の計算予定（メモ）

・異なる時間変動するポテンシャルの境界面がある場合

プログラムソース（C++）

・http://www.natural-science.or.jp/files/physics/QuantumPhysics18.cpp
※VisualC++、GCC（MinGW）で動作確認しています。