【機械学習基礎研究6】
倒立状態維持の強化学習（操作間隔を伸ばすと激むずに）
ここまで倒立状態維持の強化学習を以下のとおり様々なパラメータで試してみました。
①貪欲性に対する成功率の変化
②割引率に対する成功率の変化
③学習率に対する成功率の変化
④成功率100%となる方策
前回、成功率が100%となる貪欲性と学習率を学習回数に応じて変化させる方策を考えました。これまでは、深く考えずに滑車を0.01秒間隔（100[Hz]）で操作していましたが、今回はこの操作間隔（行動時間間隔）を0.05秒（20Hz）に伸ばしてみました。すると成功率はほぼ０になってしまいました。成功率を上げるために、次の２つを導入します。
（１）利得の再定義
→ 倒立状態は速度が０なため、「利得＝位置エネルギー」から「利得＝位置エネルギー－運動エネルギー」として運動を抑制させる
（２）環境数と行動数の最適な値を探索
Q学習のパラメータ
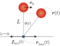
環境と行動と利得の定義（行動価値関数の定義）
・角度の分割数（環境数）：１０
・力の分割数（行動数）：１１
→ 最適行動価値関数１０×１１
利得はおもりの位置エネルギーから運動エネルギーを引いた値（$mgz-1/2 mv^2$）とし、目標達成（５秒間落下しない）やペナルティー（５秒以内に落下）は今回も与えないことにします。
Q学習の表式とパラメータの値
\begin{align} Q^{(i+1)}(s,a) \leftarrow Q^{(i)}(s,a)+\eta\left[ r+\gamma \max\limits_{a'} Q^{(i)}(s',a') -Q^{(i)}(s,a) \right] \end{align}
$s$ ： 時刻tにおける状態。$s(t)$と同値。
$a$ ： 時刻tにおける行動。$a(t)$と同値。
$r$ ： 時刻tの行動で得られた利得。$r(t+1)$と同値。
$Q(s, a)$ ： 状態$s$における行動aに対する行動価値関数。上付き添字（$i$）は学習回数を表す。
$\gamma$ ： 割引率（$0< \gamma \le 1$）
$\eta$ ： 学習率（$0< \eta \le 1$）
$s'=s(t+1)$
今回の設定
行動時間間隔：0.05（0.05秒ごとに行動を選択・実行する）
学習回数（episode）：10000
割引率（$\gamma$）: 1.0
貪欲性（$\epsilon$）:学習回数0回から5000回まで0.5から1.0まで徐々に上げる。それ以降1.0のまま
学習率（$eta$）：学習回数0回から5000回まで0.1、それ以降0.01のまま。
学習結果
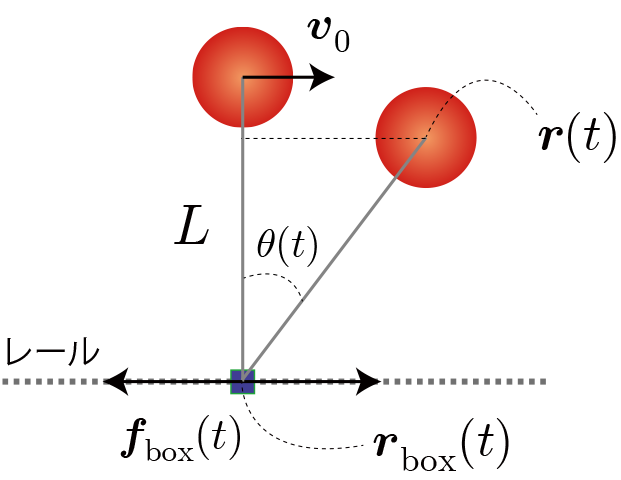
学習回数に対する成功率（100回学習ごとの平均）のグラフを示します。 同じ条件で１０回の学習し、①最も成績が良い結果（青色）、②最も成績が悪い結果（橙色）、③１０回の平均（茶色）の３つを表示します。
環境数４×行動数３
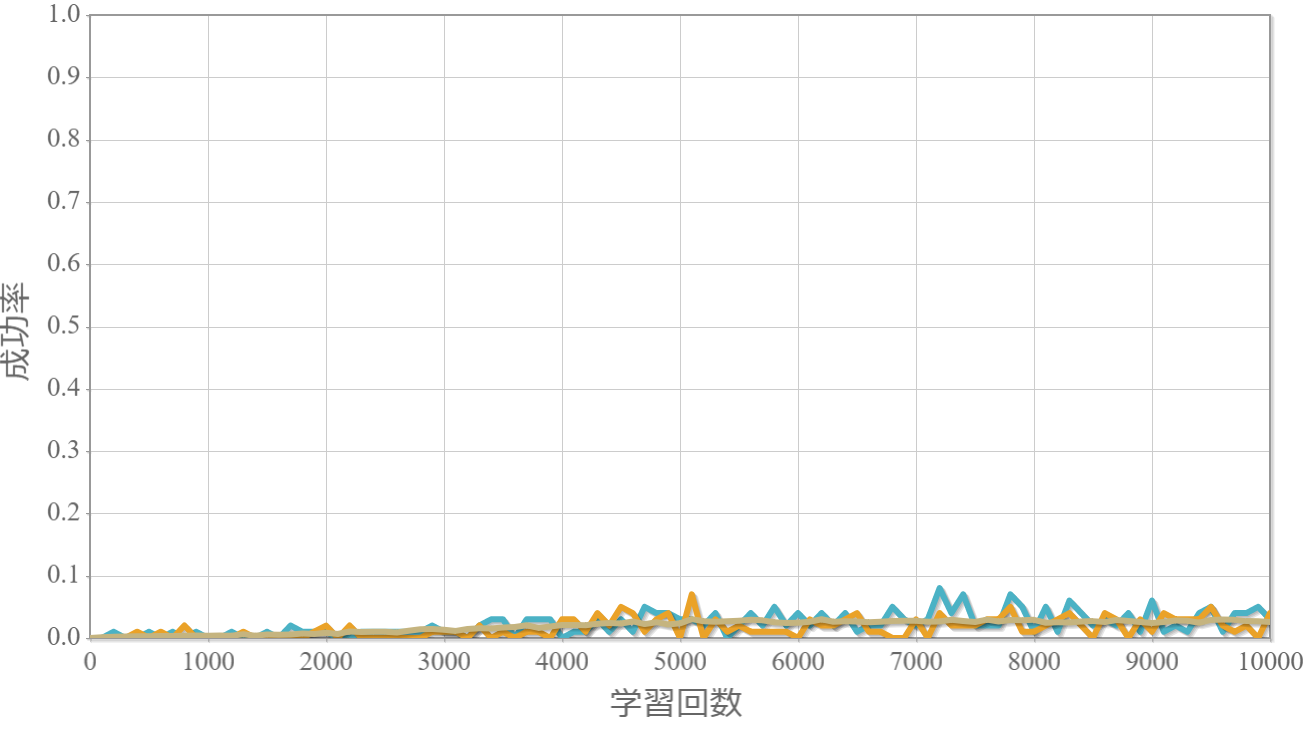
環境数１０×行動数１１
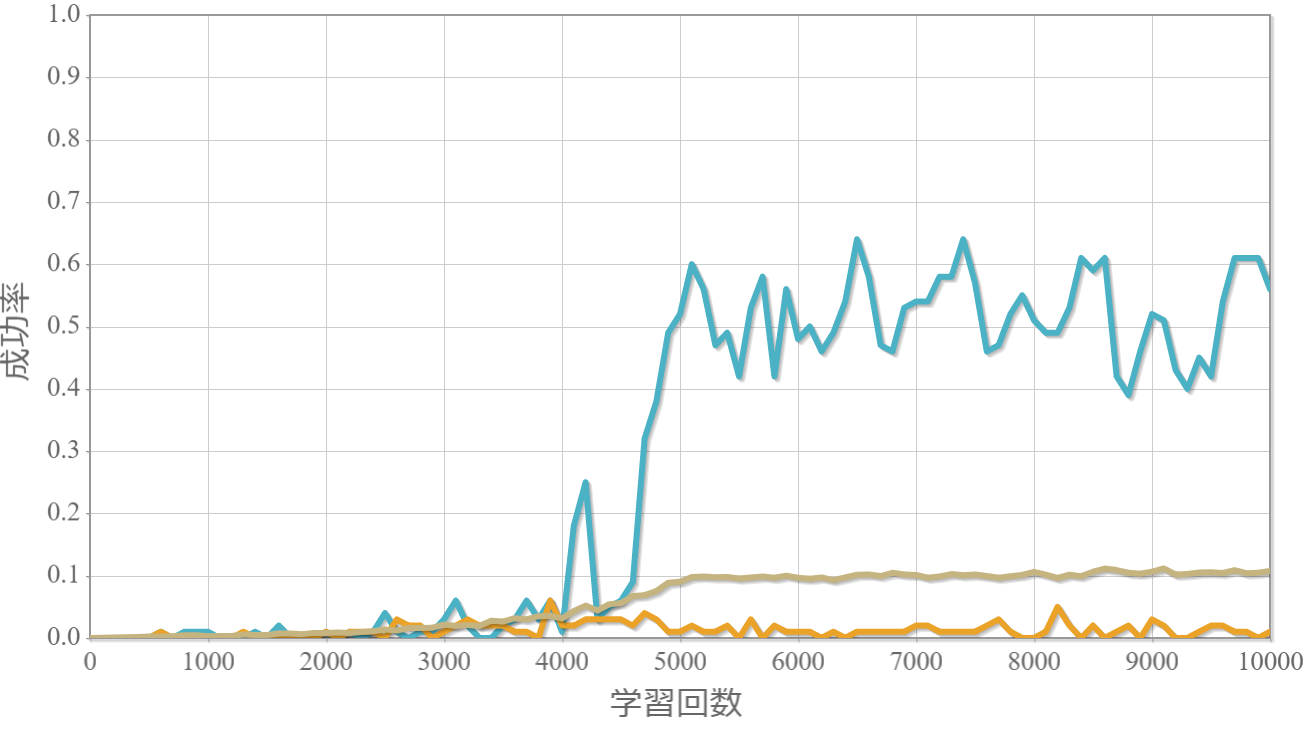
環境数１０×行動数２１
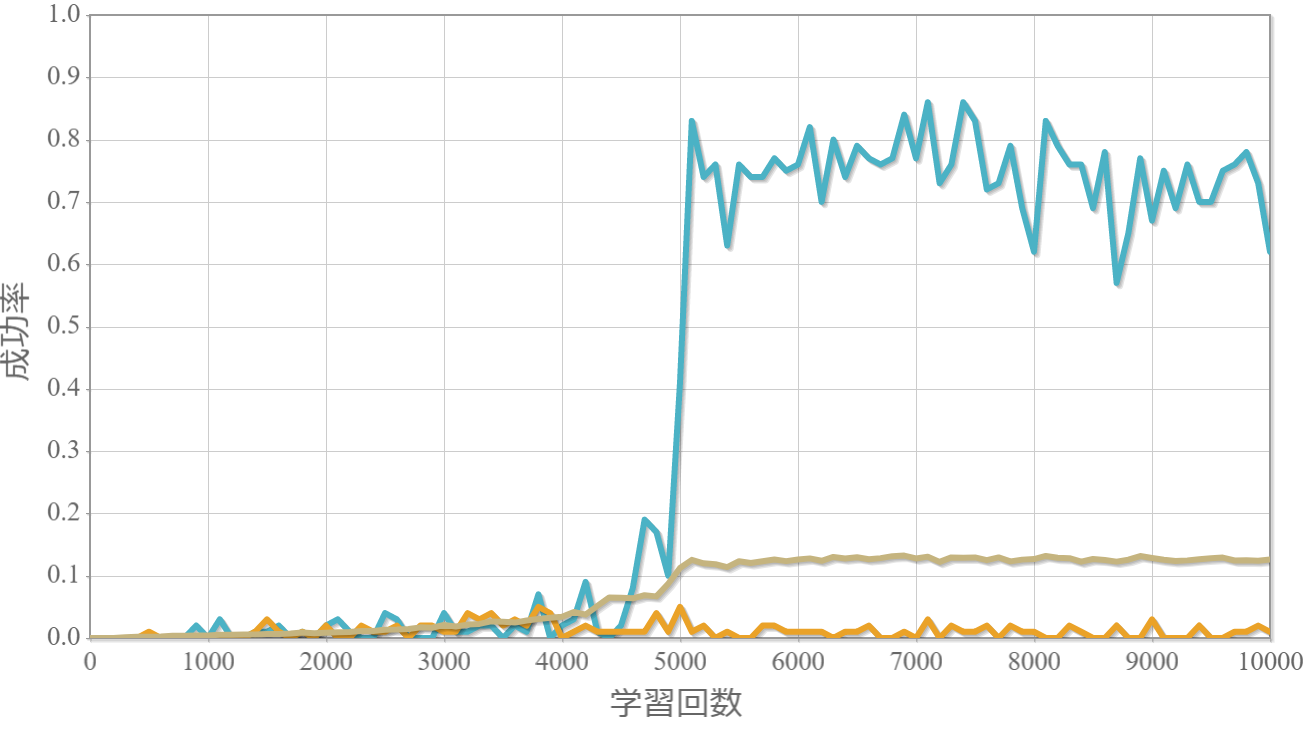
環境数１２×行動数２１
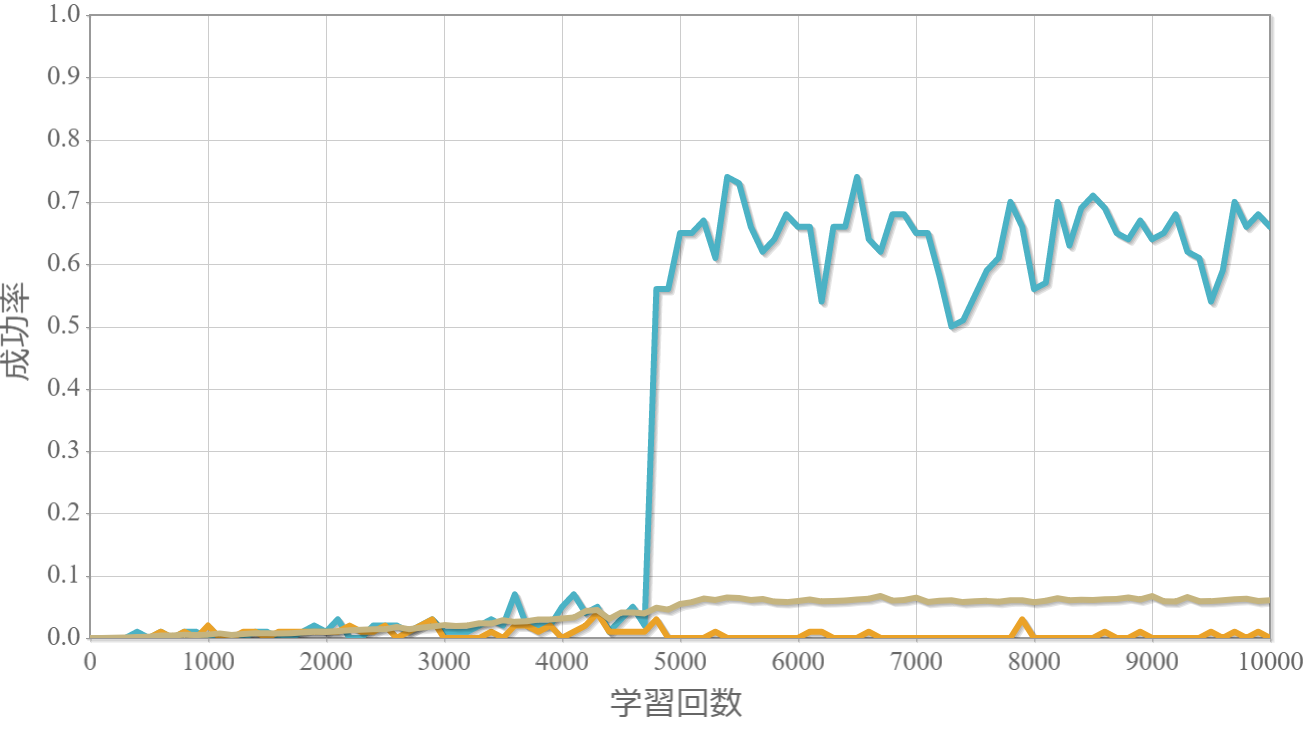
環境数１４×行動数２１
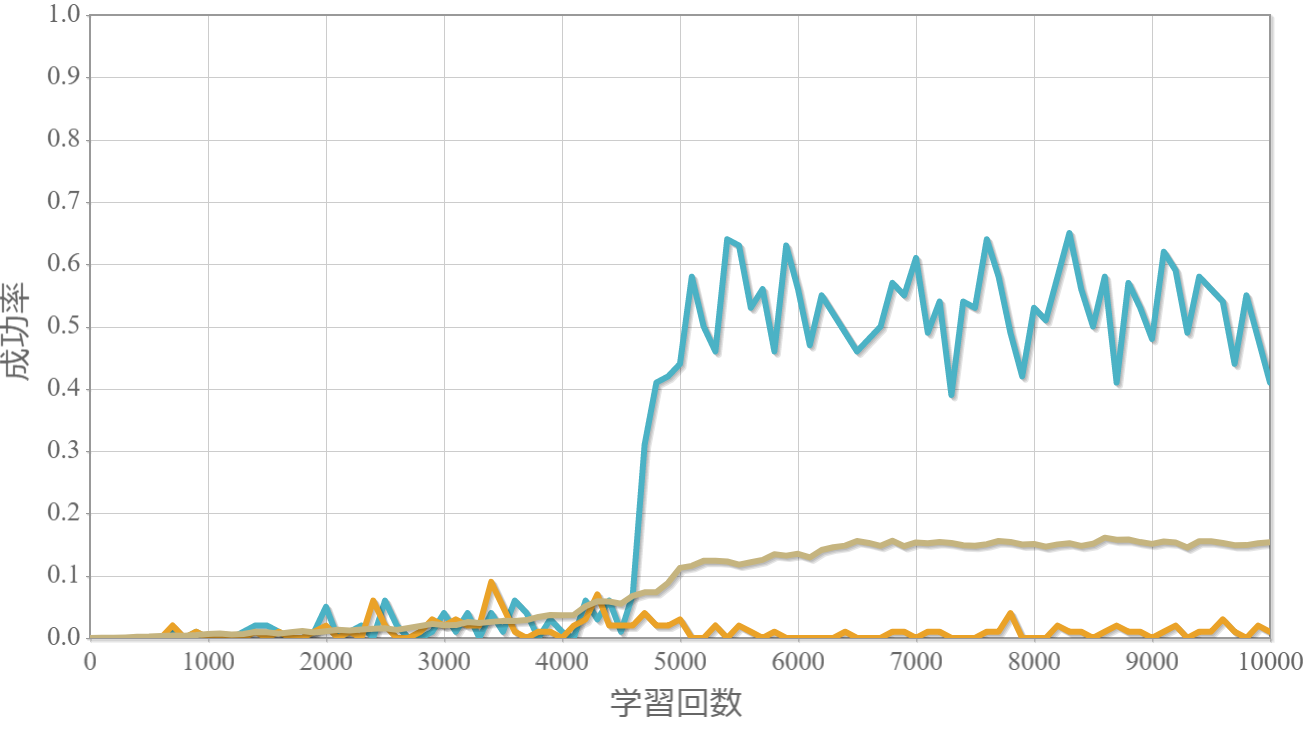
環境数１６×行動数２１
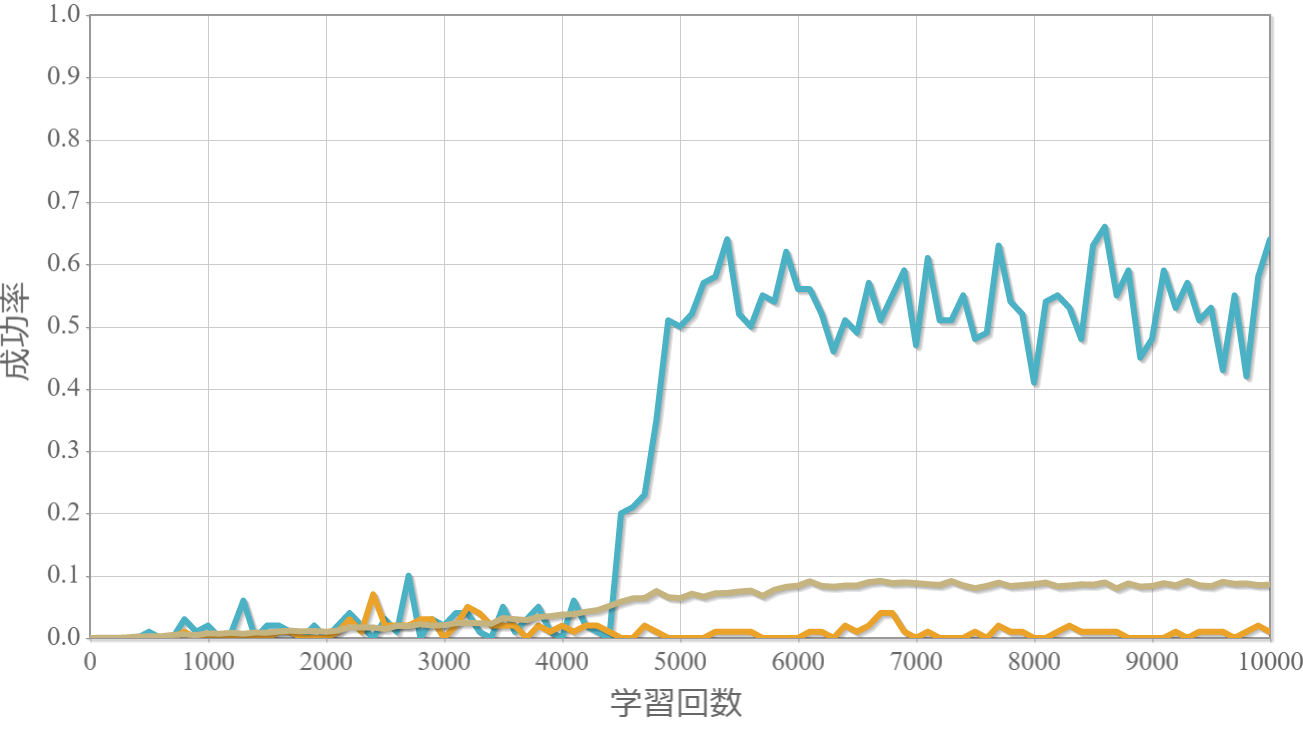
環境数２０×行動数１１
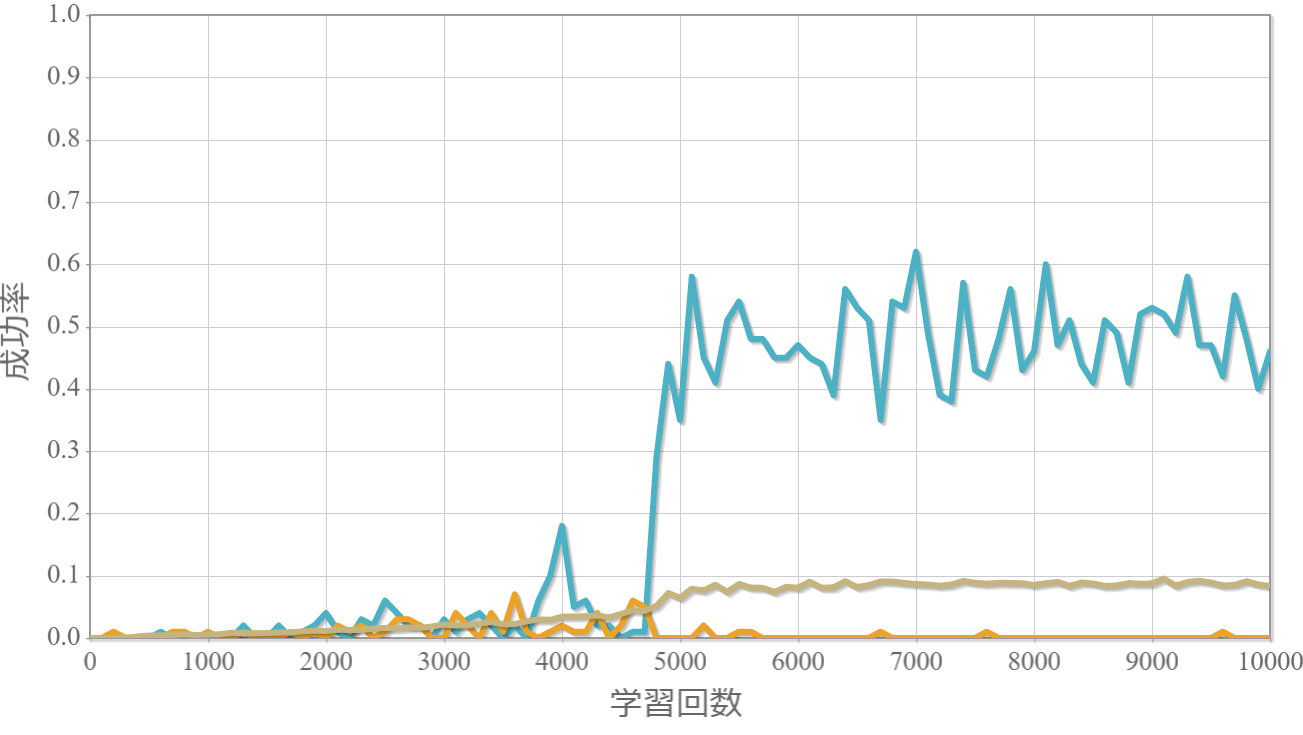
環境数２０×行動数１３
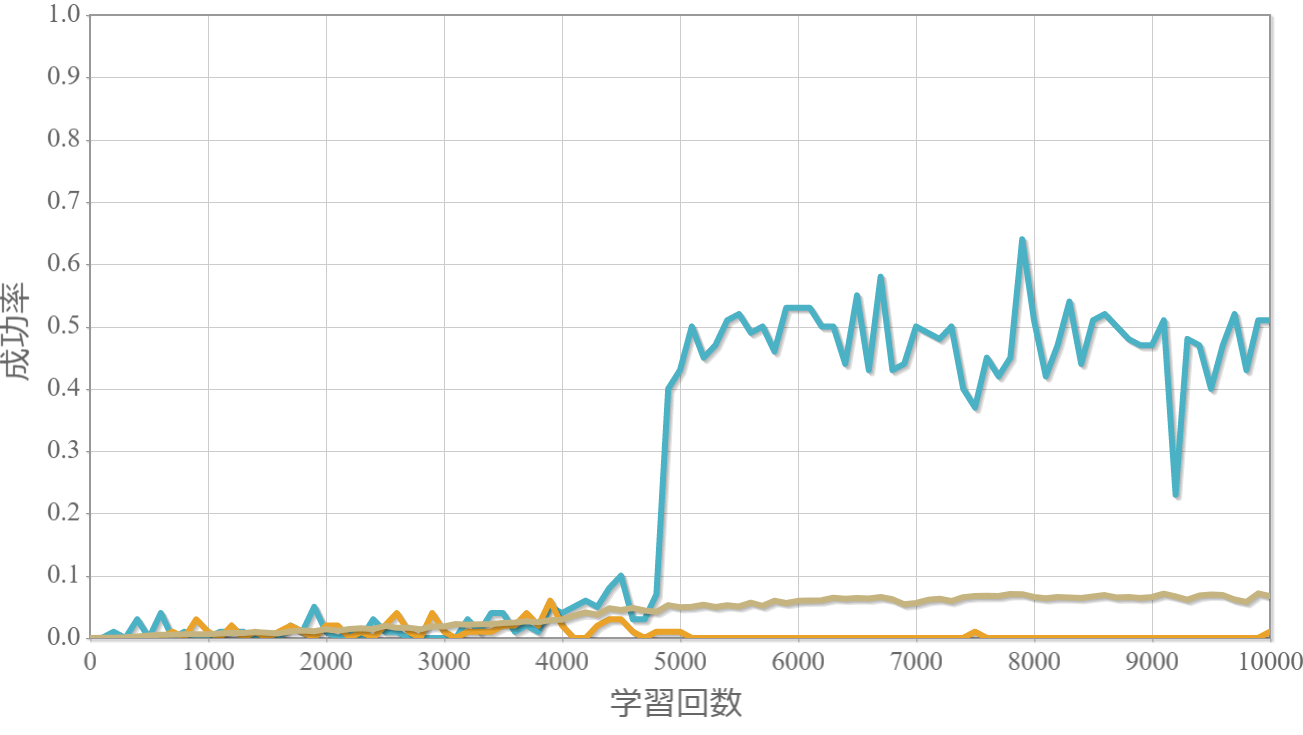
環境数２０×行動数１５
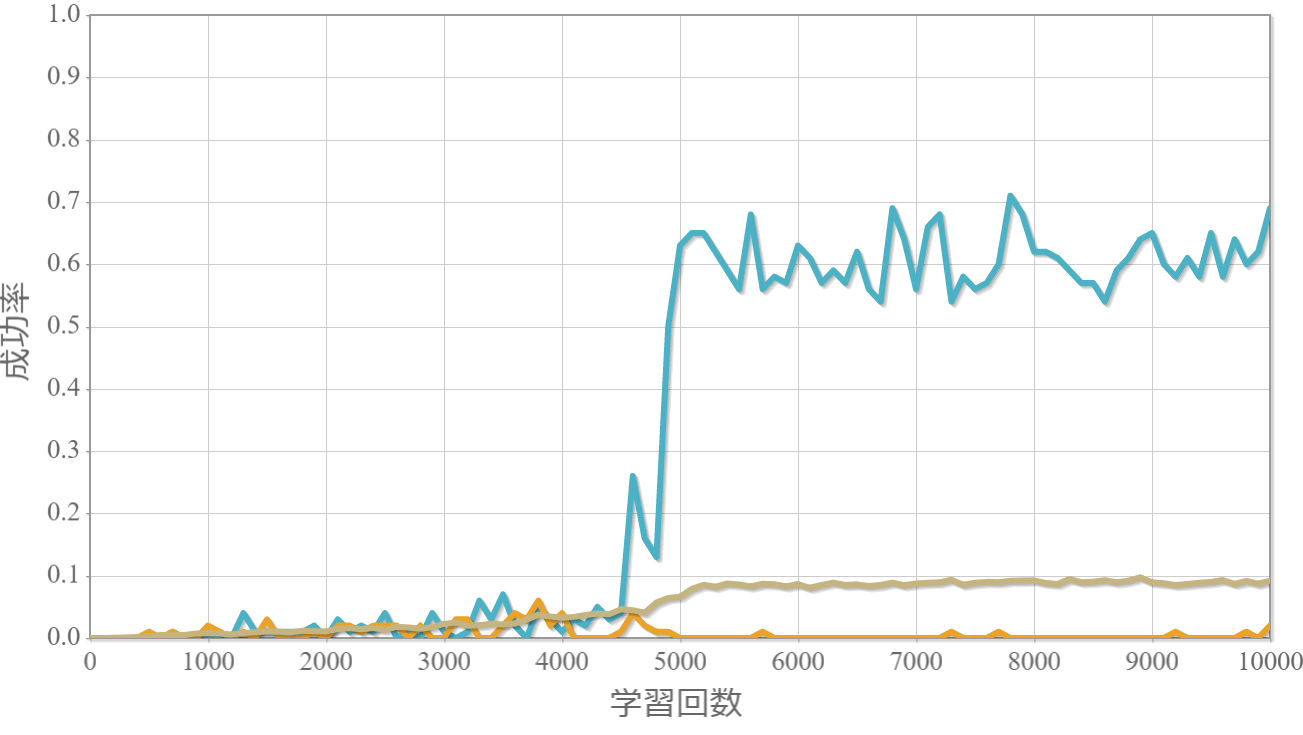
環境数２０×行動数１７
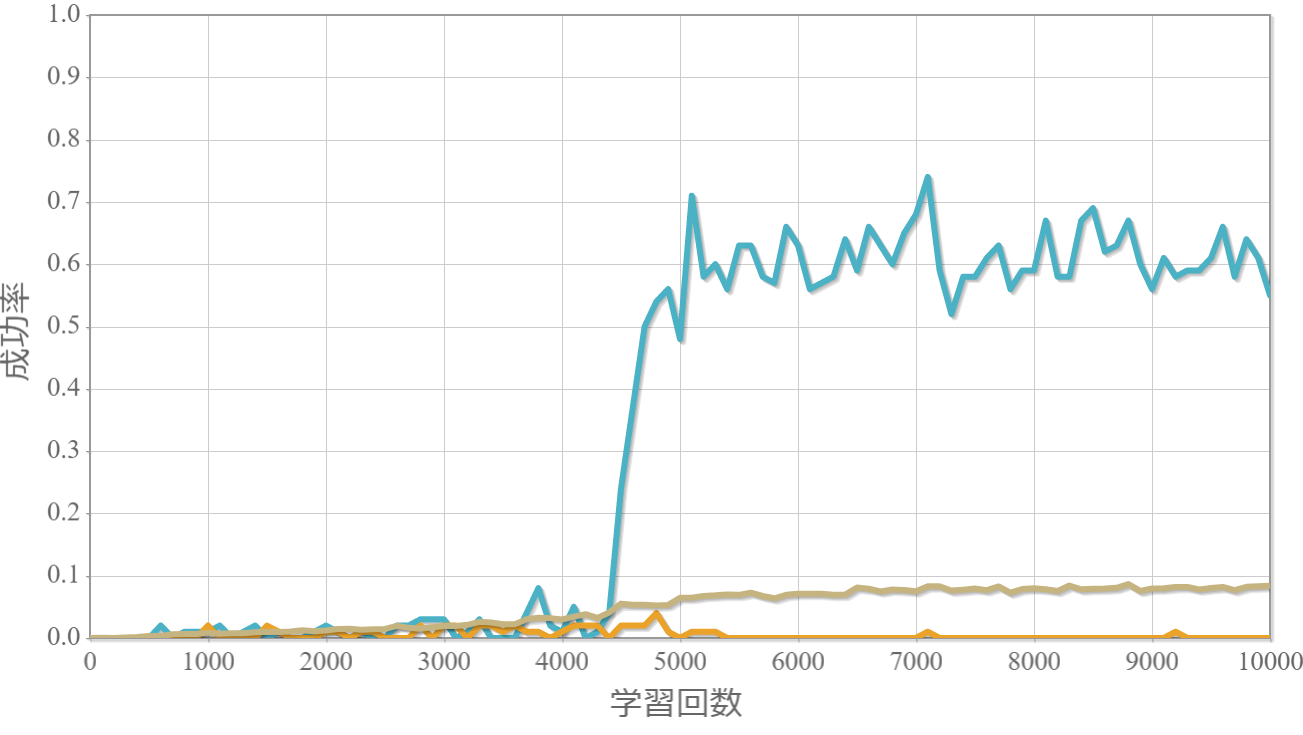
環境数１４×行動数１５
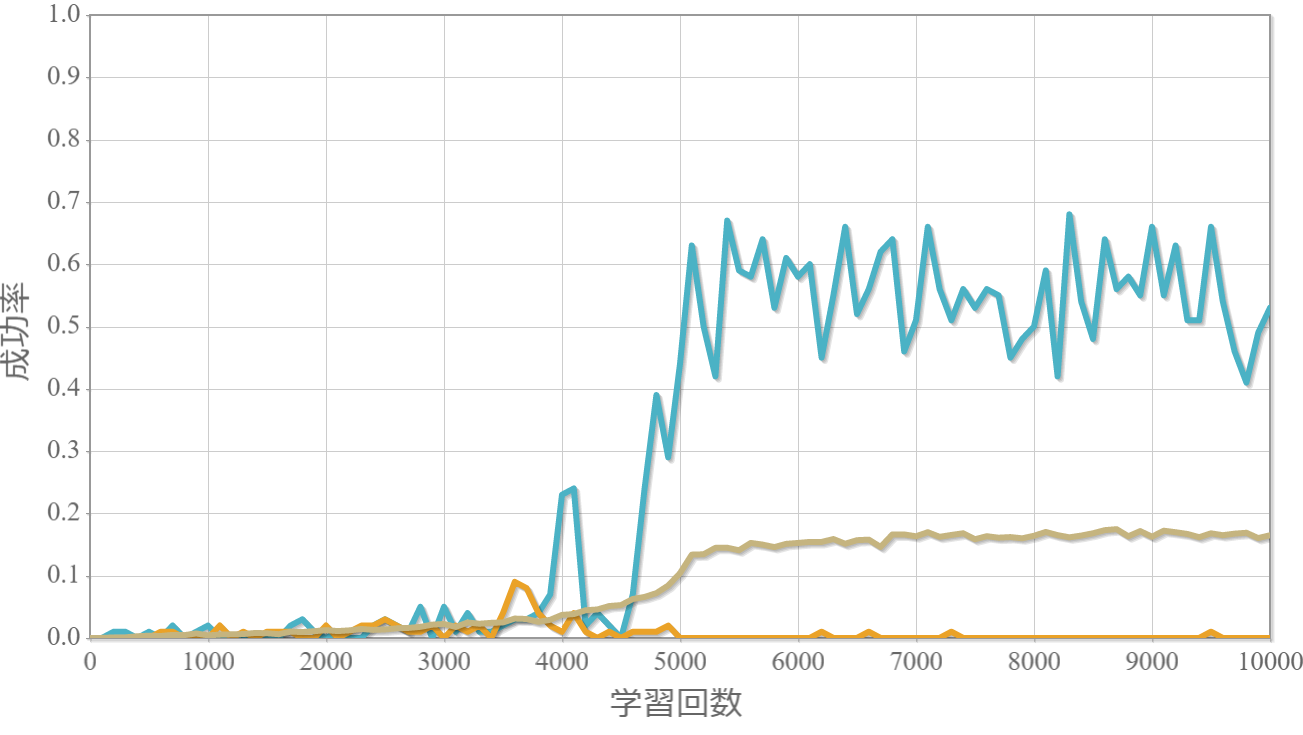
環境数１４×行動数１７
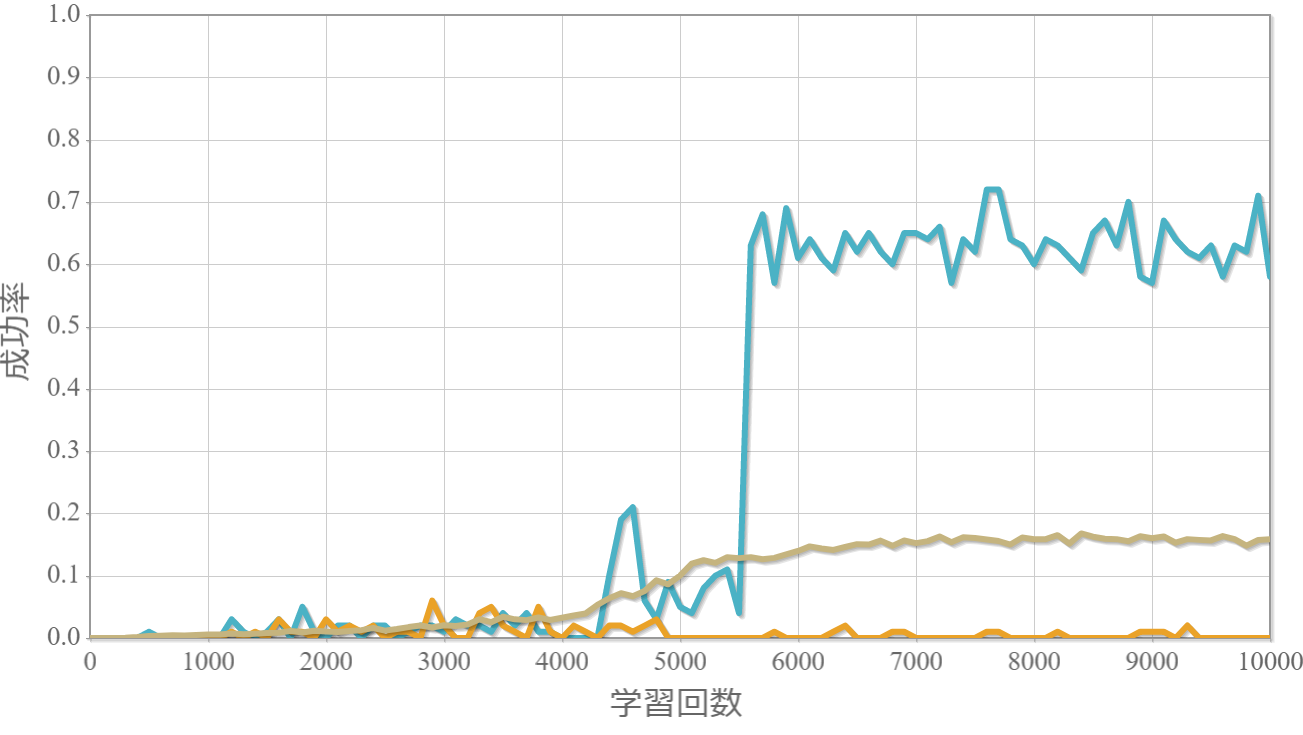
環境数１６×行動数１７
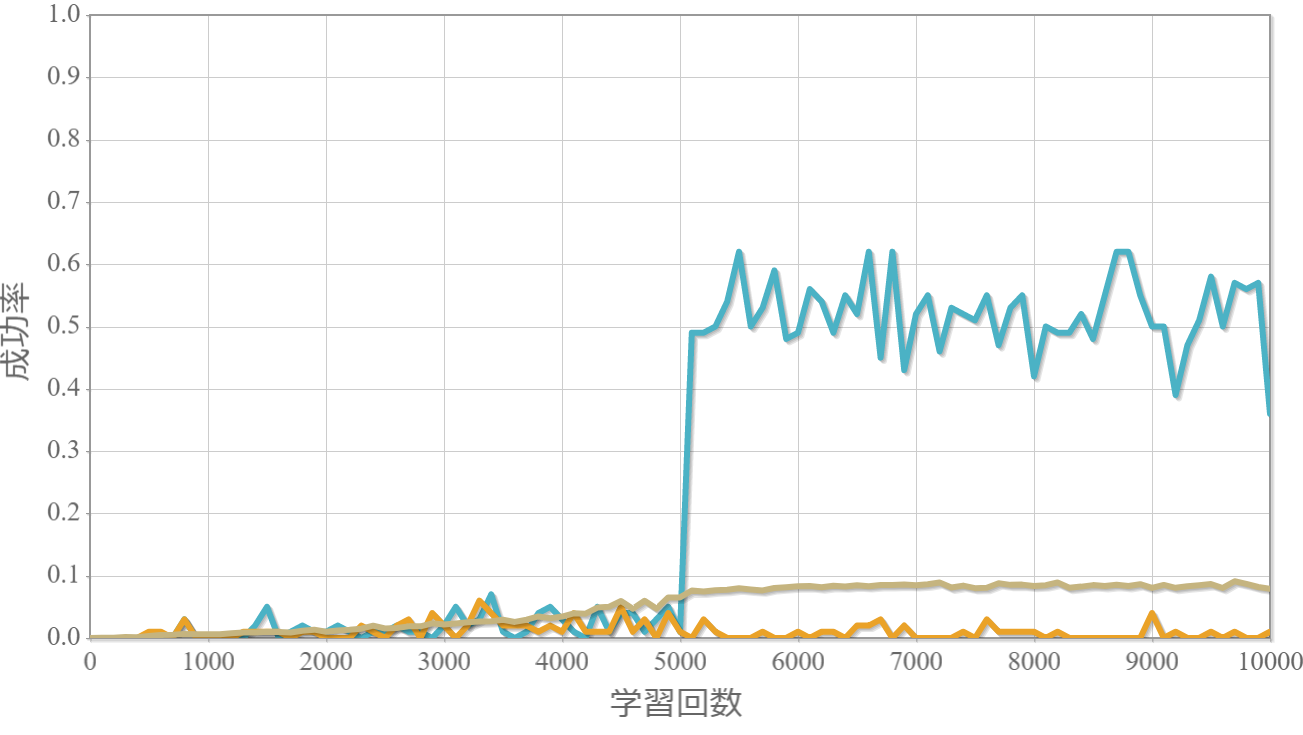
水平自由単振子運動の軌跡（滑車とおもり）（落下）
結果と考察とメモ
・行動時間間隔（操作間隔）を0.01秒から0.05秒とすると成功率は途端に下がる。
→ 利得を目的に応じて改善することで若干ましになる。
・環境数１４・行動数１５の場合が一番（それでも平均して１８％程度）良かった。
【メモ】成功率が100%となる方策を考える。
【メモ】ランダムな外力を加えて問題の難易度を上げる
プログラムソース（C++）
・http://www.natural-science.or.jp/files/NN/20180615-1.zip
※VisualStudio2017のソルーションファイルです。GCC（MinGW）でも動作確認しています。
参考（物理シミュレーション）
上記シミュレーションは、ルンゲ・クッタ法という常微分方程式を解くアルゴリズムを用いてニュートンの運動方程式を数値的に解いています。本稿で紹介した物理シミュレーションの方法を詳しく解説している書籍です。もしよろしければ「ルンゲ・クッタで行こう！～物理シミュレーションを基礎から学ぶ～（目次）」を参照ください。
