【GSLで数値計算2】
二重適応型積分による汎用数値積分を実行しよう!
本稿では、GSL(GNU科学技術計算ライブラリ)を用いて数値積分を行う方法の解説とサンプルプログラムを示します。
→ GNU科学技術計算ライブラリのインストール(Windows, VisualStudio2017)はこちら
数値積分とは?
区間[a, b]の被積分関数 $f(x) w(x)$($w(x)$は重み関数で通常は1)の積分値
\begin{align} I = \int_a^b f(x) w(x) dx \end{align}を数値的に計算することを指します。解析解には得ることができない場合に対して数値解を得るために行われます。GSLでは被積分関数の性質によって次の関数が用意されています。
・非適応型ガウス・クロンロッド積分(QNG)
・適応型ガウス・クロンロッド積分(QAG)
・特異点に対応した適応型積分(QAGS)
・特異点が分かっている関数に対する適応型積分(QAGP)
・無限区間に対する適応型積分計算(QAGI)
・コーシーの主値の適応型積分(QAWC)
・特異点を持つ関数のための適応型積分(QAWS)
・振動する関数のための適応型積分(QAWO)
・フーリエ積分のための適応型積分(QAWF)
・二重適応型積分(CQUAD)
・ロンバーグ積分
・ガウス・ルジャンドル積分
・Fixed point quadratures
上記の名称で「適応型」とあるのは被積分関数の形に依って分点の数を決める自動積分法を意味します。本稿ではこの中で最も汎用性の高い「二重適応型積分(CQUAD)」による数値積分を紹介します。
二重適応型積分(CQUAD)の利用方法
二重適応型積分とは
CQUADは、ほとんどのタイプの特異点、InfやNaNなどの非数値関数値、およびいくつかの分岐積分を扱うことができる新しい二重適応型と呼ばれるの数値積分法です。 一般に、QUADPACKの他の計算法よりも多くの関数評価が必要ですが、困難な被積分関数でもあまり失敗しません。
二重適応型積分のサンプルプログラム
本家マニュアルにあるサンプルプログラムに加筆したプログラムを以下に示します。 被積分関数の特異点が積分区間の下端に存在する
\begin{align} I = \int_0^1 \frac{\log(\alpha x)}{\sqrt{x}} dx \end{align}の積分を計算しています。解析値は-4です。
//////////////////////////////////////////////////////////////////////// //数値積分:二重適応型積分(CQUAD) //////////////////////////////////////////////////////////////////////// #include#include #include #include //被積分関数の定義 double f(double x, void * params) { //計算パラメータ double alpha = *(double *)params; //被積分関数 double f = log(alpha*x) / sqrt(x); return f; } int main(void) { //積分結果と推定誤差を保持する作業領域 gsl_integration_cquad_workspace * w = gsl_integration_cquad_workspace_alloc(100); //計算結果取得用変数 double result, error; //評価回数取得用変数 size_t nevals; //理論値 double expected = -4.0; //被積分関数のパラメータ double alpha = 1.0; //GSLにおくる被積分関数の構造体 gsl_function F = { &f, &alpha }; //CQUAD 二重適応型積分 gsl_integration_cquad( &F, //被積分関数の定義 0, 1.0, //積分範囲(a,b) 0, 1e-10, //収束させる推定絶対誤差と相対誤差 w, //作業領域のサイズと 作業領域 &result, //計算結果取得 &error, //推定絶対誤差取得 &nevals //評価回数取得 ); std::cout << "【計算結果】" << std::endl; std::cout << std::setprecision(15); std::cout << "計算結果 = " << result << std::endl; std::cout << "理論値 = " << expected << std::endl; std::cout << "推定絶対誤差 = " << error << std::endl; std::cout << "評価回数 = " << nevals << std::endl; std::cout << "計算誤差 = " << result - expected << std::endl; std::cout << "積分区間の分割数 = " << w->size << std::endl; //作業領域の解放 gsl_integration_cquad_workspace_free(w); std::string s; std::cin >> s; return 0; }
実行結果
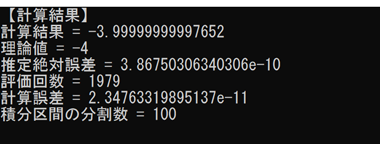
指定した誤差以内の数値積分の結果を得ることができました。
































