【GSLで数値計算3】
モンテカルロ積分による汎用数値積分を実行しよう！

本稿では、GSL（GNU科学技術計算ライブラリ）を用いて数値積分を行う方法の解説とサンプルプログラムを示します。 → GNU科学技術計算ライブラリのインストール（Windows, VisualStudio2017）はこちら

モンテカルロ積分とは

モンテカルロ積分とは被積分関数の積分区間の値をランダムの参照して積分値を推定する計算アルゴリズムです。 積分変数が多数ある多重積分で有用となります。

\begin{align} I = \int_{x_1}^{x_0}dx\int_{y_1}^{y_0}dy \cdots f(x, y, \cdots) \end{align}

GSLではモンテカルロ積分に３つのアルゴリズムが用意されています。

・標準：積分区間内からサンプル点をランダムに選ぶ
・MISER法：積分区間内で推定積分値の分散がもっとも大きな領域に集中してサンプル点を選ぶ
・被積分関数の絶対値に比例した確率でサンプル点を選ぶ

モンテカルロ積分の利用方法

二重適応型積分のサンプルプログラム

本家マニュアルにあるサンプルプログラムに加筆したプログラムを以下に示します。 被積分関数は積分区間の端に特異点が存在します。

\begin{align} I = \int_{-\pi}^\pi \frac{dk_x}{2\pi} \int_{-\pi}^\pi \frac{dk_y}{2\pi} \int_{-\pi}^\pi \frac{dk_z}{2\pi} \frac{1}{1-\cos(k_x)\cos(k_y)\cos(k_z)} \end{align}

解析解は$\Gamma(1/4)^4/(4\pi^3) = 1.3932039296856768591842462603255$です。

 
////////////////////////////////////////////////////////////////////////
//モンテカルロ積分
////////////////////////////////////////////////////////////////////////
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

double exact = 1.3932039296856768591842462603255;
double g(double *k, size_t dim, void *params) {
	double A = 1.0 / (M_PI * M_PI * M_PI);
	return A / (1.0 - cos(k[0]) * cos(k[1]) * cos(k[2]));
}
void display_results(std::string title, double result, double error) {
	std::cout << " ========" << title.c_str() << "==========" << std::endl;
	std::cout << std::setprecision(8) << std::scientific;
	std::cout << "計算結果 = " << result << std::endl;
	std::cout << "理論値 = " << exact << std::endl;
	std::cout << "σ = " << error << std::endl;
	std::cout << "error = " << result - exact << " = " << fabs(result - exact) / error << "σ" << std::endl;
}
int main(void) {
	double res, err;
	double xl[3] = { 0, 0, 0 };
	double xu[3] = { M_PI, M_PI, M_PI };
	//乱数発生器のタイプのインスタンス
	const gsl_rng_type *T; 
	//乱数発生器のインスタンス
	gsl_rng *r;
	//被積分関数を規定する構造体
	gsl_monte_function G = { &g, 3, 0 };
	//被積分関数の評価回数
	size_t calls = 500000;              
	//乱数発生器の初期化
	gsl_rng_env_setup();
	//乱数発生器のタイプとして「gsl_rng_default」を指定
	T = gsl_rng_default;
	//指定した乱数発生器のインスタンスを生成
	r = gsl_rng_alloc(T);                
	{
		//モンテカルロ積分の作業領域の確保（）
		gsl_monte_plain_state *s = gsl_monte_plain_alloc(3);
		gsl_monte_plain_integrate(&G, //被積分関数 
			xl, //積分区間の下限
			xu, //積分区間の上限
			3,  //積分変数の次元
			calls, //評価回数
			r,  //乱数発生器のインスタンス
			s,  //モンテカルロ積分の作業領域
			&res, //計算結果
			&err);//推定絶対誤差
		gsl_monte_plain_free(s);
		display_results("plain", res, err);
	}
	{
		//miser法
		gsl_monte_miser_state *s = gsl_monte_miser_alloc(3);
		gsl_monte_miser_integrate(&G, xl, xu, 3, calls, r, s, &res, &err);
		gsl_monte_miser_free(s);
		display_results("miser", res, err);
	}
	{
		//vegas 法
		gsl_monte_vegas_state *s = gsl_monte_vegas_alloc(3);
		gsl_monte_vegas_integrate(&G, xl, xu, 3, 10000, r, s, &res, &err);
		std::string title = "vegas warm-up";
		display_results(title, res, err);

		std::cout << "収束待ち..." << std::endl;
		do {
			gsl_monte_vegas_integrate(&G, xl, xu, 3, calls / 5, r, s, &res, &err);
			std::cout << "計算結果 = " << res << "  σ = " << err  << "chisq/dof =" << s->chisq << std::endl;
		} while (fabs(s->chisq - 1.0) > 0.5);

		display_results("vegas final", res, err);
		gsl_monte_vegas_free(s);
	}
	gsl_rng_free(r);

	std::string s;
	std::cin >> s;
	return 0;
}
}

実行結果

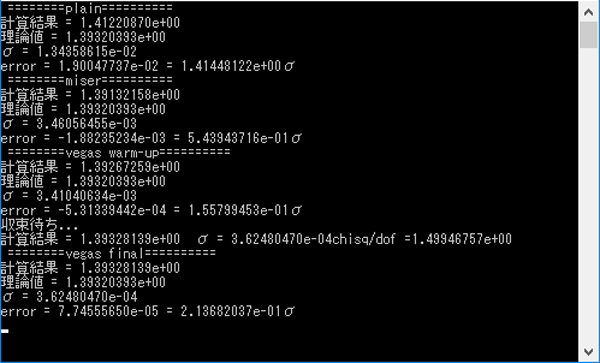
特異点のある３重積分で、誤差を$10^{-4}$（vegas法）に抑えて、問題なく積分できることが確認できました。