【GSLで数値計算5】
実対称行列の固有値の固有ベクトルを計算

本稿では、GSL（GNU科学技術計算ライブラリ）を用いて実対称行列の固有値と固有ベクトルの計算を行うサンプルプログラムを示します。→ GNU科学技術計算ライブラリのインストール（Windows, VisualStudio2017）はこちら

 
//////////////////////////////////////////
// 実対称行列の固有値の固有ベクトル
//////////////////////////////////////////
#include 
#include 
#include 
#include 
#include 
#include 
#include 

//行列の次元
const int DIM = 4;

int main(void) {

	// 行列の準備
	double data[] = {
		1.0 / 1.0, 1.0 / 2.0, 1.0 / 3.0, 1.0 / 4.0,
		1.0 / 2.0, 1.0 / 3.0, 1.0 / 4.0, 1.0 / 5.0,
		1.0 / 3.0, 1.0 / 4.0, 1.0 / 5.0, 1.0 / 6.0,
		1.0 / 4.0, 1.0 / 5.0, 1.0 / 6.0, 1.0 / 7.0
	};
	// GSL行列の生成
	gsl_matrix_view m = gsl_matrix_view_array(data, DIM, DIM);
	// GSLベクトルの生成（固有値用）
	gsl_vector *eval = gsl_vector_alloc(DIM);
	// GSLベクトルの生成（固有ベクトル用）
	gsl_matrix *evec = gsl_matrix_alloc(DIM, DIM);
	// 対象行列計算用メモリ確保
	gsl_eigen_symmv_workspace * w = gsl_eigen_symmv_alloc(DIM);
	// 固有値と固有ベクトルを計算
	gsl_eigen_symmv(
		&m.matrix, //行列
		eval,      //固有値
		evec,      //固有ベクトル
		w          //ワークスペース
	);
	//対象行列計算用メモリの解放
	gsl_eigen_symmv_free(w);
	//固有値の大きさに合わせて並び替え
	gsl_eigen_symmv_sort(eval, evec, GSL_EIGEN_SORT_ABS_ASC);

	for (int i = 0; i < DIM; i++) {
		//i番目の固有値を取得
		double eval_i = gsl_vector_get(eval, i);

		std::cout << i + 1 << "番目の固有値 = " << eval_i << std::endl;
		std::cout << i + 1 << "番目の固有ベクトル" << std::endl;
		for (int j = 0; j < DIM; j++) {
			//縦ベクトルを取得
			double v_ji = gsl_matrix_get(evec, j, i);
			std::cout << "  " << v_ji << std::endl;
		}
		//i番目の固有ベクトルを取得
		//gsl_vector_view evec_i = gsl_matrix_column(evec, i);
		//gsl_vector_fprintf(stdout, &evec_i.vector, "%g");
	}

	///////////////////////////////////////
	// 検算　MX-XE = 0
	///////////////////////////////////////
	double _data[] = {
		1.0 / 1.0, 1.0 / 2.0, 1.0 / 3.0, 1.0 / 4.0,
		1.0 / 2.0, 1.0 / 3.0, 1.0 / 4.0, 1.0 / 5.0,
		1.0 / 3.0, 1.0 / 4.0, 1.0 / 5.0, 1.0 / 6.0,
		1.0 / 4.0, 1.0 / 5.0, 1.0 / 6.0, 1.0 / 7.0
	};
	// GSL行列の生成
	gsl_matrix_view M_view = gsl_matrix_view_array(_data, DIM, DIM);
	gsl_matrix *M = &M_view.matrix;

	// XEを計算するための準備（縦に固有値を並べる）
	double e_data[DIM*DIM];
	for (int i = 0; i < DIM; i++) {
		for (int j = 0; j < DIM; j++) {
			e_data[i*DIM + j] = gsl_vector_get(eval, j);
		}
	}
	// GSL行列の生成（XE）
	gsl_matrix_view XE_view = gsl_matrix_view_array(e_data, DIM, DIM);
	gsl_matrix *XE = &XE_view.matrix;
	//行列要素同士の積を計算→ XEが完成
	gsl_matrix_mul_elements(XE, evec);

	// C = \alpha {\rm op}(M) {\rm op}(X) + \beta XE
	gsl_blas_dgemm(
		CblasNoTrans, // 行列Aの変換 {\rm op}(A)（※１）
		CblasNoTrans, // 行列Bの変換 {\rm op}(B)（※１） 
		1.0,          // alpha
		M,            // M
		evec,         // X
		-1.0,         // beta
		XE            // 戻り値
	);
	//（※１）変換なし：CblasNoTrans, 転置：CblasTrans, エルミート転置：CblasConjTrans


	std::cout << std::endl << "-----検算結果-----" << std::endl;
	for (int i = 0; i < DIM; i++) {
		for (int j = 0; j < DIM; j++) {
			std::cout << XE->data[i*DIM + j] << " ";
		}
		std::cout << std::endl;
	}

	//領域の開放
	gsl_vector_free(eval);
	gsl_matrix_free(evec);

	std::string s;
	std::cin >> s;
	return 0;
}

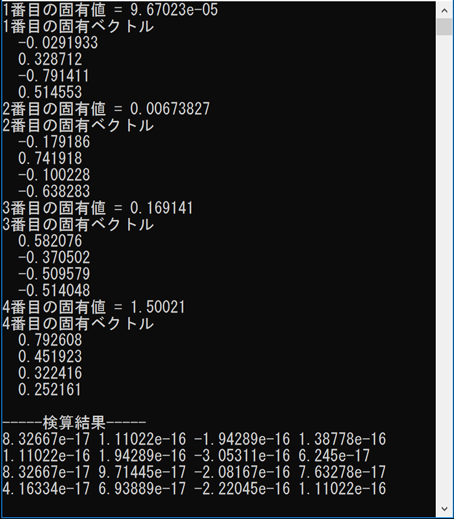
実行結果