【機械学習基礎研究16】
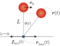
最下点からの倒立状態への強化学習の３次元グラフィックス
「最下点からの強制振動で倒立状態への強化学習（利得の与え方と学習手順）」で計算した最適行動評価関数を用いて、最下点から強制振動で倒立状態を維持する強化学習の結果を３次元グラフィックスで可視化します。
結果と考察とメモ
・最適行動評価関数がシンプルすぎるせいか３０秒まではうまく行っているが、経験が未熟な状況（？）に至るとうまく対処できていない。
→ 利得の与え方が２モード（最下点からの強制振動と倒立維持）しか用意していないためと考えられる。
【メモ】減点に向かって収束させるにはどのような学習が必要なのか？ → モードを追加する。
【メモ】最適行動評価関数にニューラルネットワークを用いた深層強化学習に取り組む
プログラムソース（C++）
・http://www.natural-science.or.jp/files/NN/20180728-1.zip
※VisualStudio2017のソルーションファイルです。GCC（MinGW）でも動作確認しています。
参考（物理シミュレーション）
上記シミュレーションは、ルンゲ・クッタ法という常微分方程式を解くアルゴリズムを用いてニュートンの運動方程式を数値的に解いています。本稿で紹介した物理シミュレーションの方法を詳しく解説している書籍です。もしよろしければ「ルンゲ・クッタで行こう！～物理シミュレーションを基礎から学ぶ～（目次）」を参照ください。
