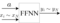【ニューラルネットワークの基礎研究31】
ニューラルネットワークによる関数近似の検証(中間層1層の場合)
ニューラルネットワークは入力値に対する出力値を教師信号として内部パラメータ(重みとバイアス)を学習させることで、任意の関数を表現することが知られています。 今更な感じですが、本稿ではニューラルネットワークではそもそもどのようにして任意の関数を近似しているのかの検証結果を示します。
近似対象の関数とニューラルネットワークの構造
ニューラルネットワークがどのように関数を表現しているかを確認するために、引数が1個の三角関数を中間層1層のニューラルネットワークで表現してみます。
対象関数
\begin{align} f(x) = \sin(2\pi x) \end{align}xの区間を0から1とします。
ニューラルネットワークの構造
・ニューラルネットワークの構造:順伝播型ニューラルネットワーク(FFNN)
・学習方法:通常の勾配法(学習率固定、逆誤差伝搬法)
・学習回数:100,000階
・学習率:eta = 0.01;
・ミニバッチ数:100 (サンプルは無限に用意できるためミニバッチという概念は存在しませんが、ランダムに用意したミニバッチ数分のサンプルに対する平均を用いて学習を進める)
・活性化関数(中間層):ReLU(ランプ関数)
・活性化関数(出力層):恒等関数
・損失関数:2乗和
中間層のニューロン数10個の学習結果
中間層のニューロン数10個のニューラルネットワークを100個独立に用意し、100,000回学習後に最も損失値(元の関数との誤差)の小さなネットワークを用いて計算した結果です。
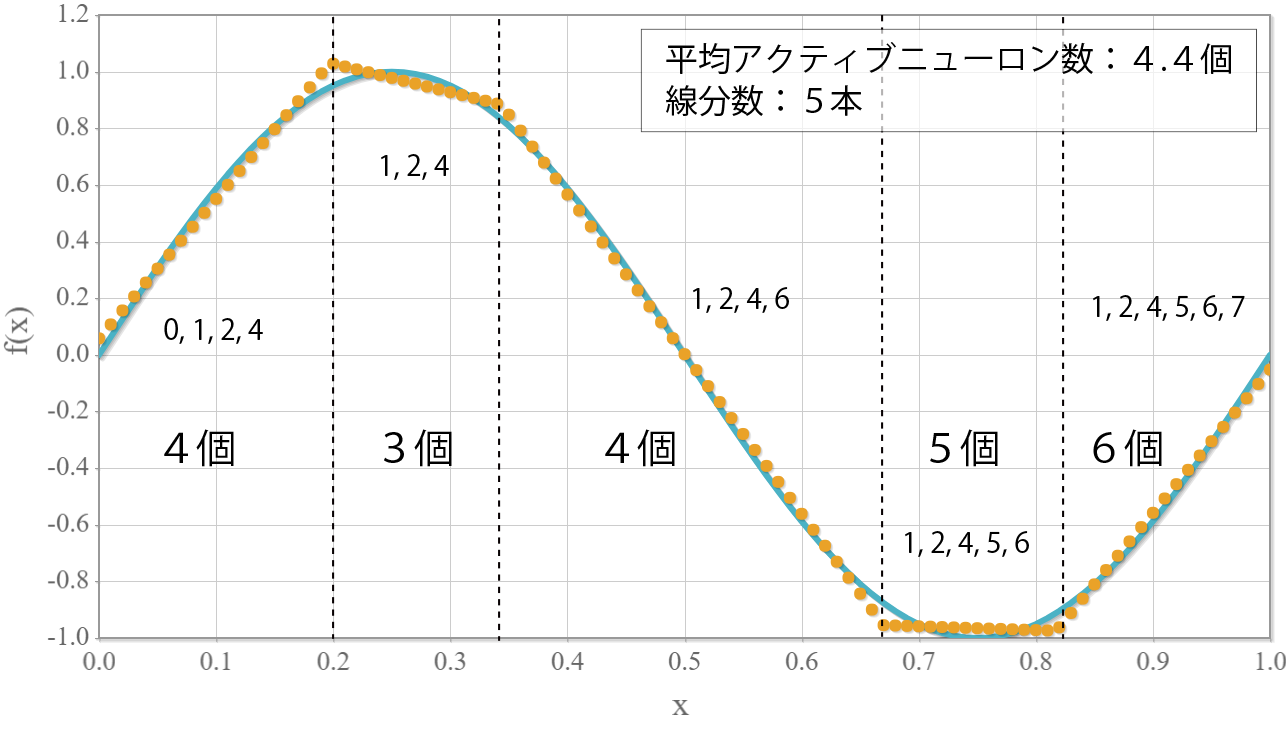
ニューラルネットワークは、全区間0から1までを5本の線分で表現していることがわかります。グラフ中に記載した番号はアクティブなニューロンの番号(0~9)とアクティブなニューロンの個数です。各線分はアクティブな3個から6個のニューロンで表現していることを示しています。ちなみに区間全体でアクティブニューロンの平均数は4.4個でした。
以上から言えることは、中間層1層のニューラルネットワークは中間層のニューロンの活性(アクティブ)/不活性(非アクティブ)を組み合わせて線分を生成することで、学習対象の関数を表現していて、中間層のニューロン数が多くなるほど線分の本数を増やすことで学習対象の関数をより精密に表現していくということです。
【疑問】線分本数やアクティブニューロン数と中間層ニューロン数の関係は?
ここで一つ疑問が湧いてきます。学習対象の関数を表現する線分本数やアクティブニューロン数と中間層ニューロン数の関係はどうなっているのかということです。 そこで、中間層のニューロン数を10個から100個まで10個ずつ増やした場合の、それらの値を調べた結果が次の図です。横軸が中間層のニューロン数、縦軸は一つがアクティブなニューロン数の平均、もう一つが線分の本数です。
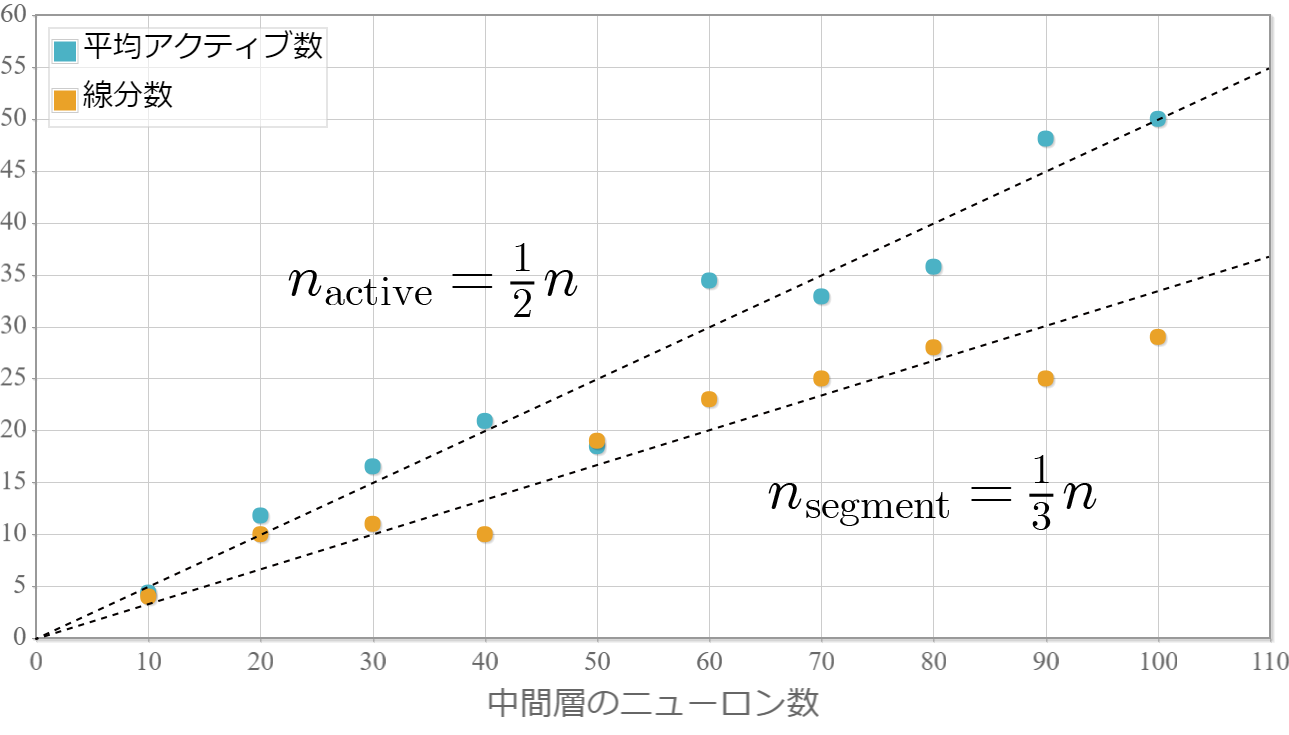
概ね、アクティブニューロン数は中間層ニューロン数の1/2、線分の本数は中間層ニューロン数の1/3という結果が出ました。 各区間でニューロン数のおおよそ半分がアクティブであるというのは意外でした。この状態がネットワークをフル活用しているという意味があるのかもしれません。 次回は、中間層の層数を増やしたときの様子を調べます。