アルゴリズム
三目並べの決勝パターン分析
3×3のマス目に○(先手)と×(後手)のマークを交互に埋めていき、縦・横・斜めのいずれかで同じマークが3つ並ぶと勝ちという2人対決ゲームがあります。
3×3=9つのマス目に「○」「×」「未配置」の3つのどれかが入ると考えると、位置まで区別すると全部で$3^9=19683$パターンの状態が存在しますが、対称性を考慮すると自明ではありません。前回の記事では勝負が決した後も9手目まで埋めましたが、今回は勝負が決した時点で終了として、何パターンの状態が存在するのかを調べました。
※ソースコードはこちら(HTMLファイル)
全譜面の列挙(対称性を考慮)
「○」→「×」→「○」→「×」→「○」→「×」→「○」→「×」→「○」 と順番に埋めていき、勝敗が決定した時点で終了とします。
0手目で決勝:0パターン

1手目で決勝:0パターン
2手目で決勝:0パターン

3手目で決勝:0パターン
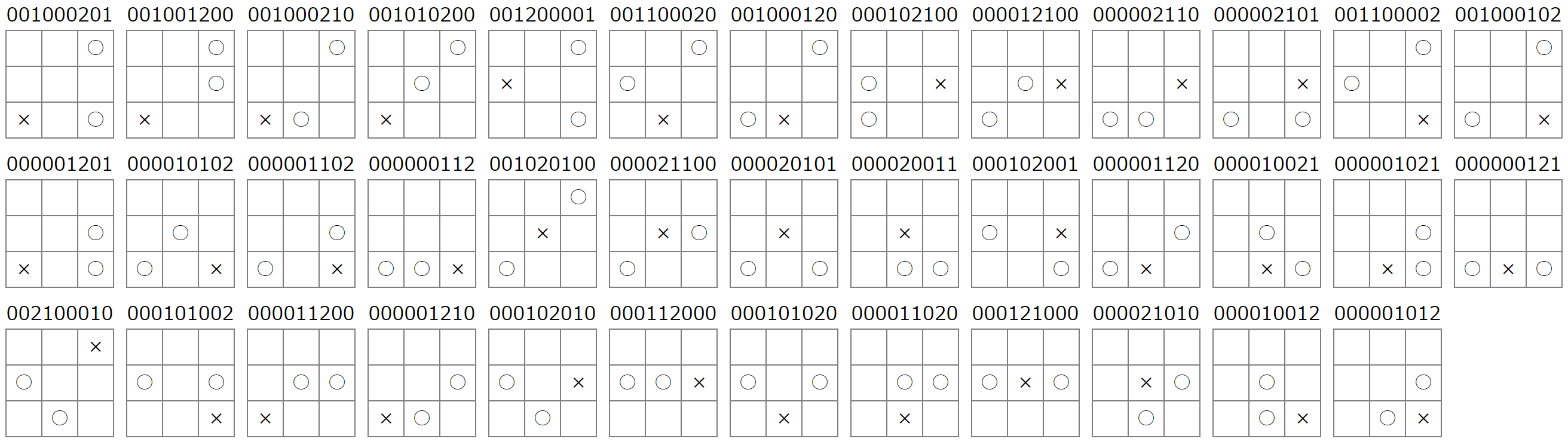
4手目で決勝:0パターン
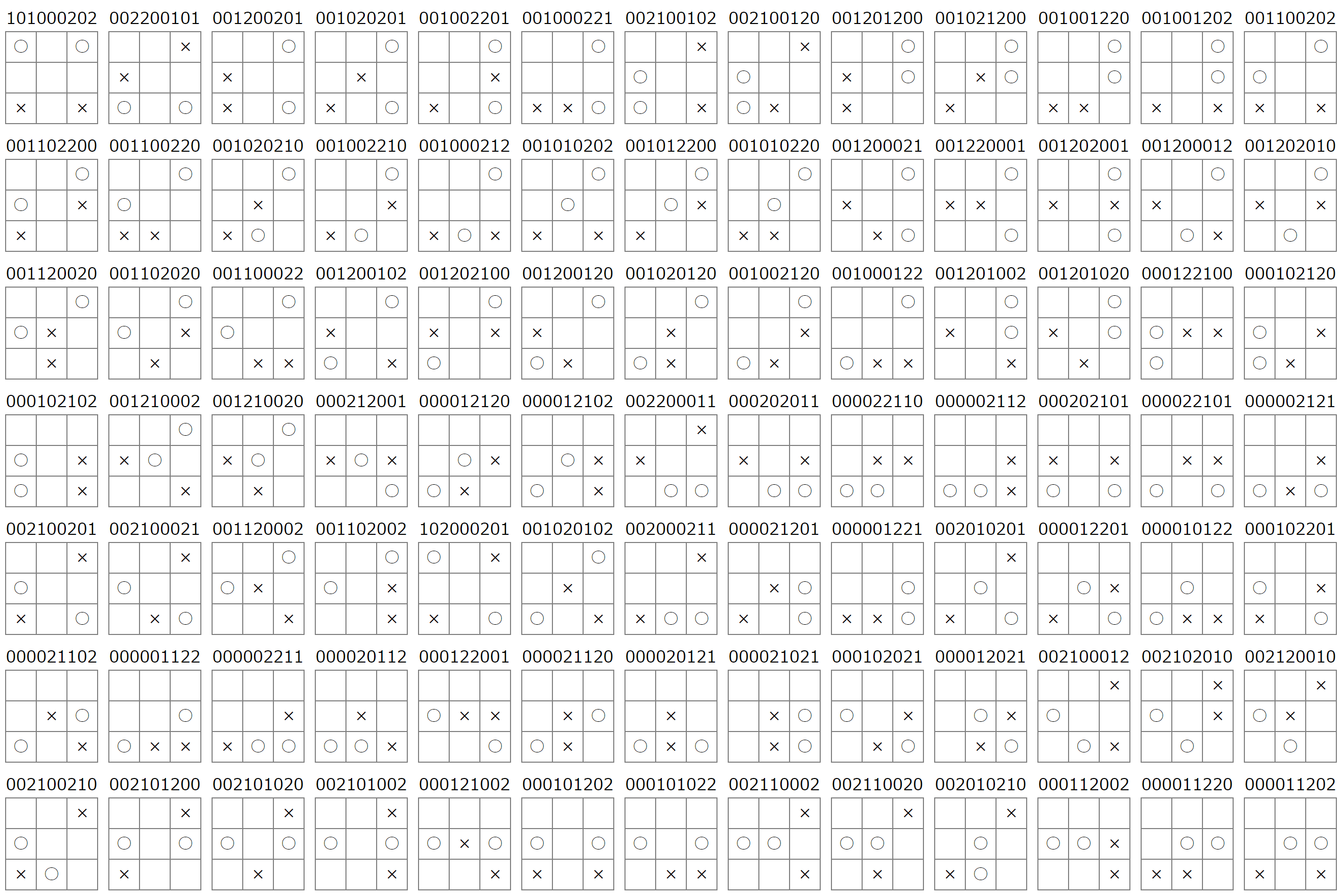

5手目で決勝:21パターン
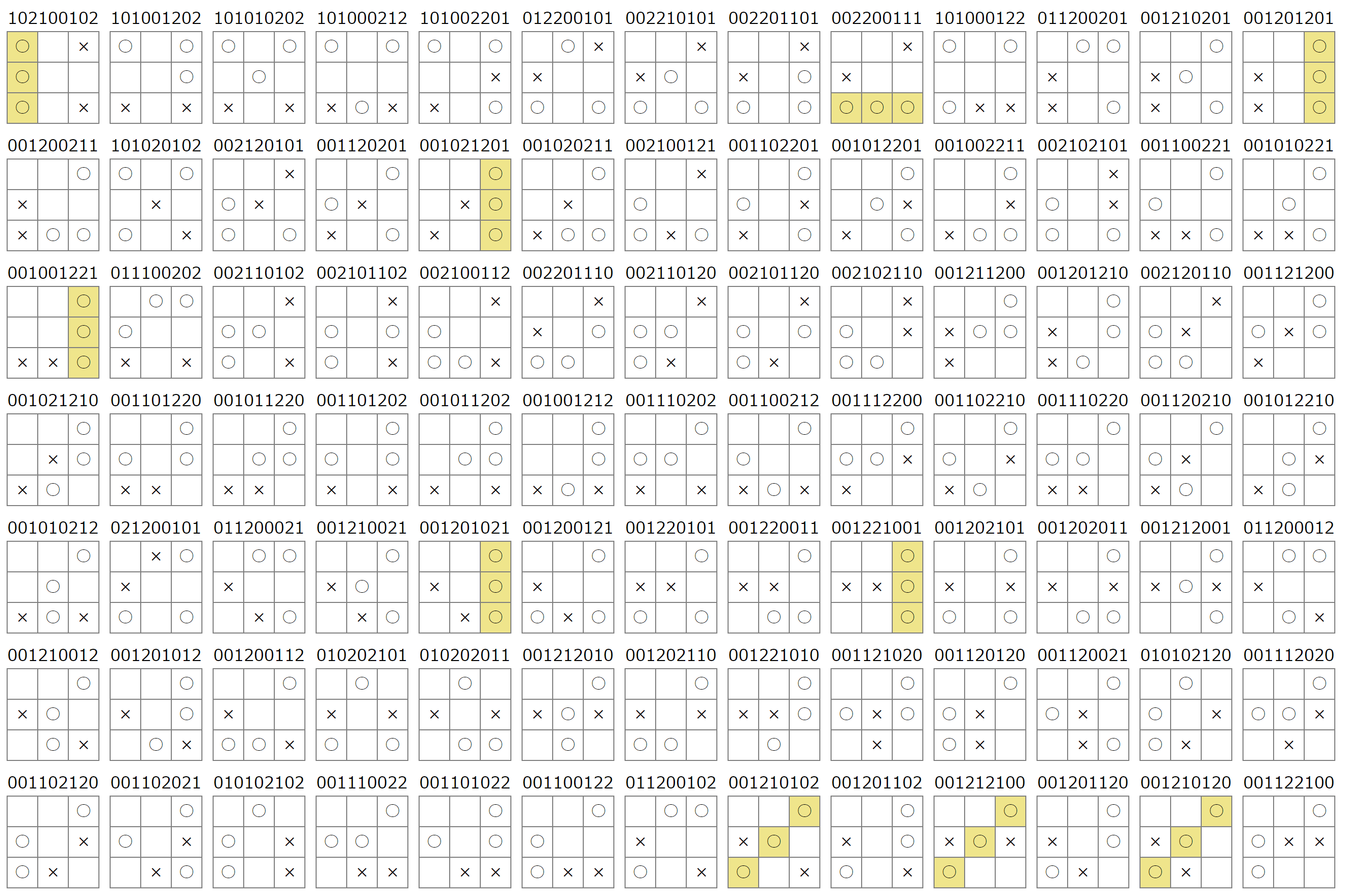
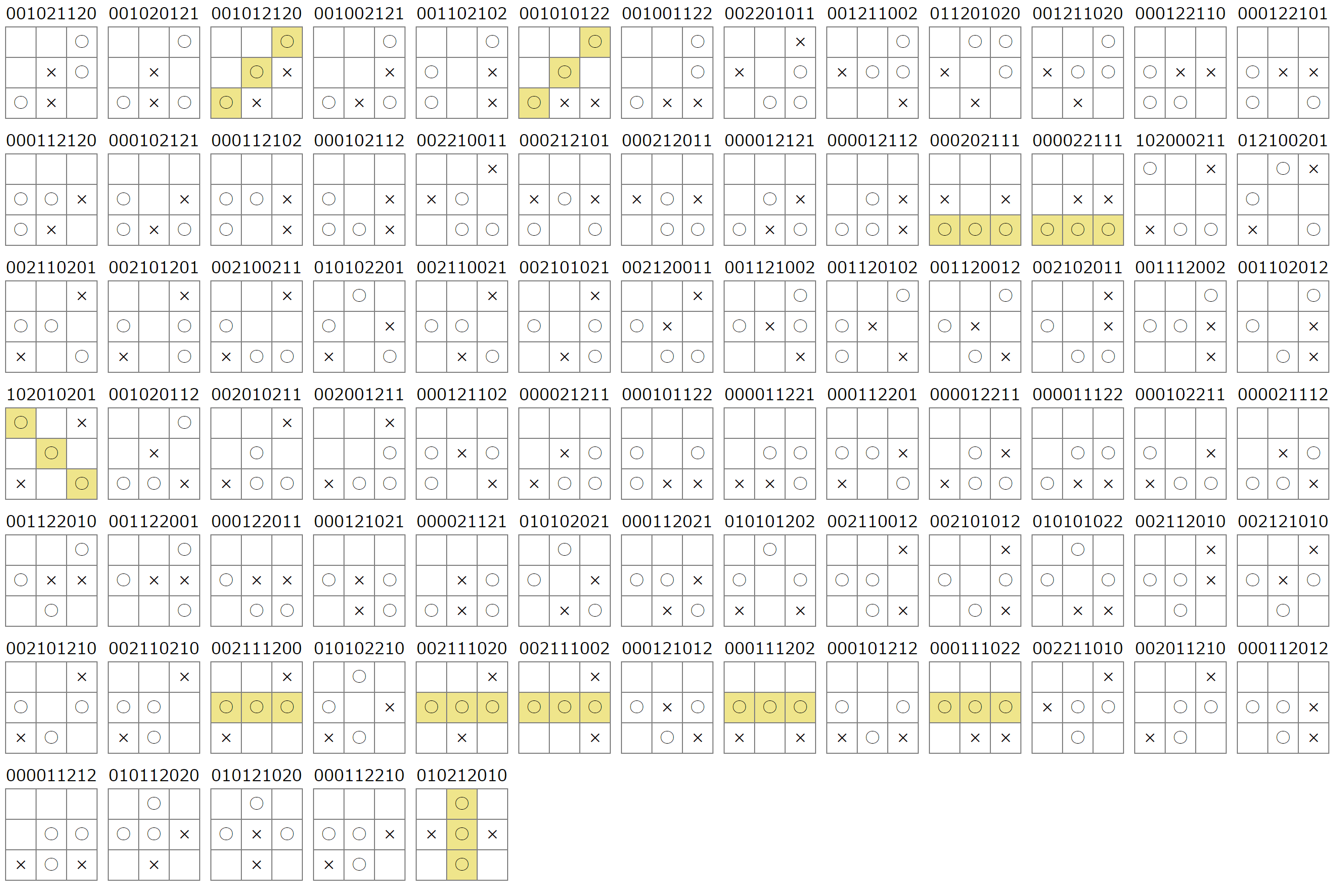
6手目で決勝:21パターン
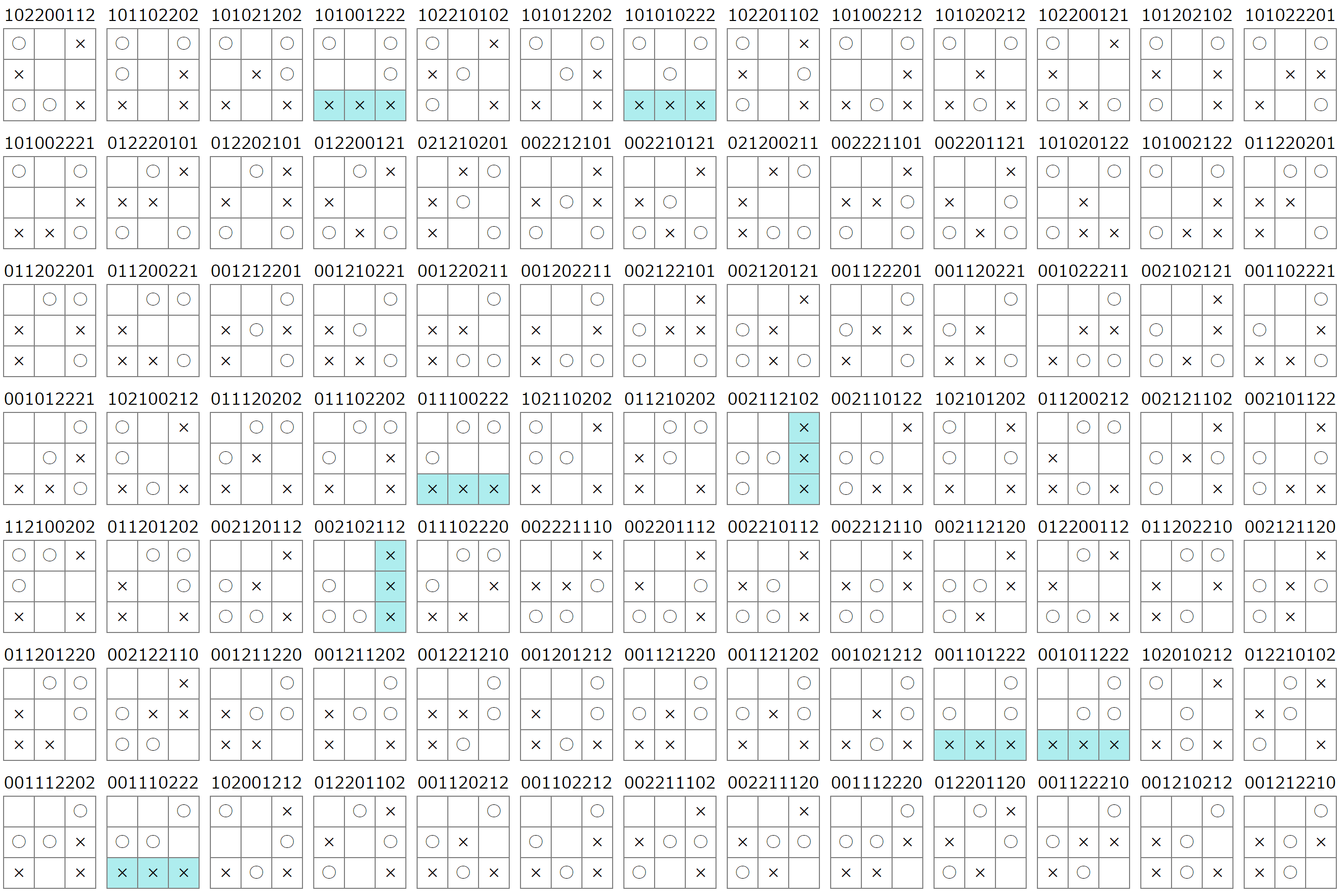
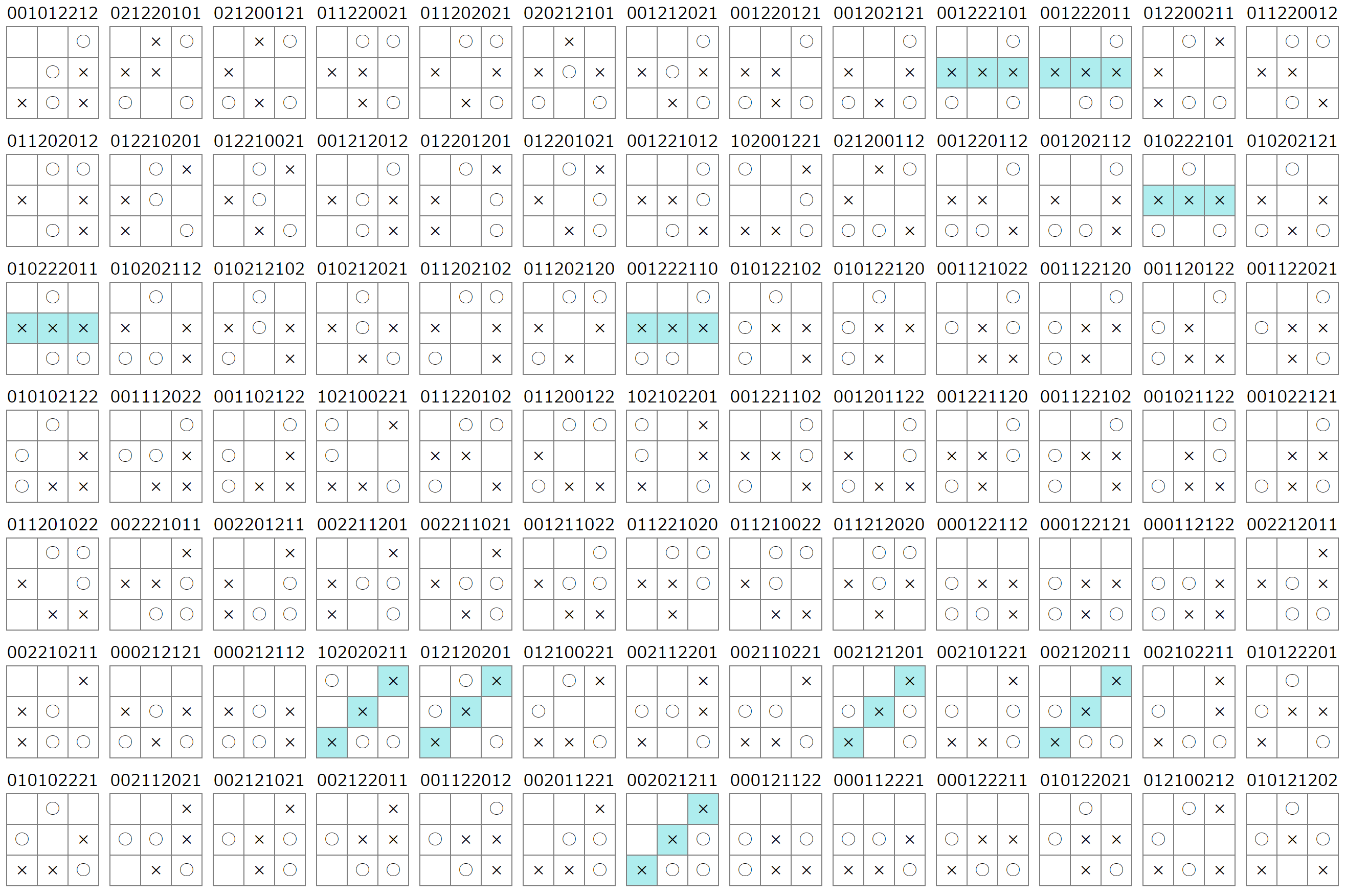

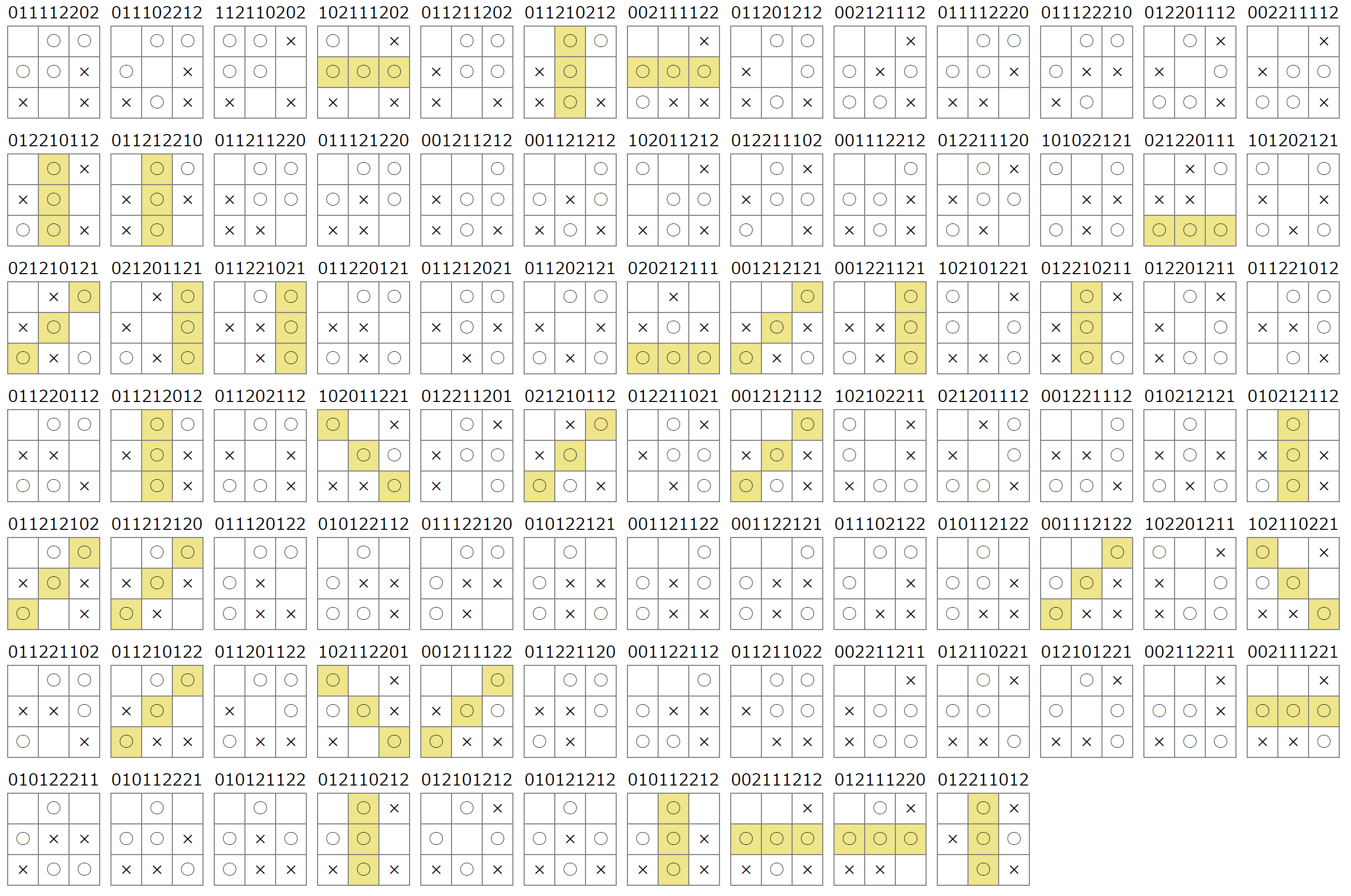
7手目で決勝:58パターン
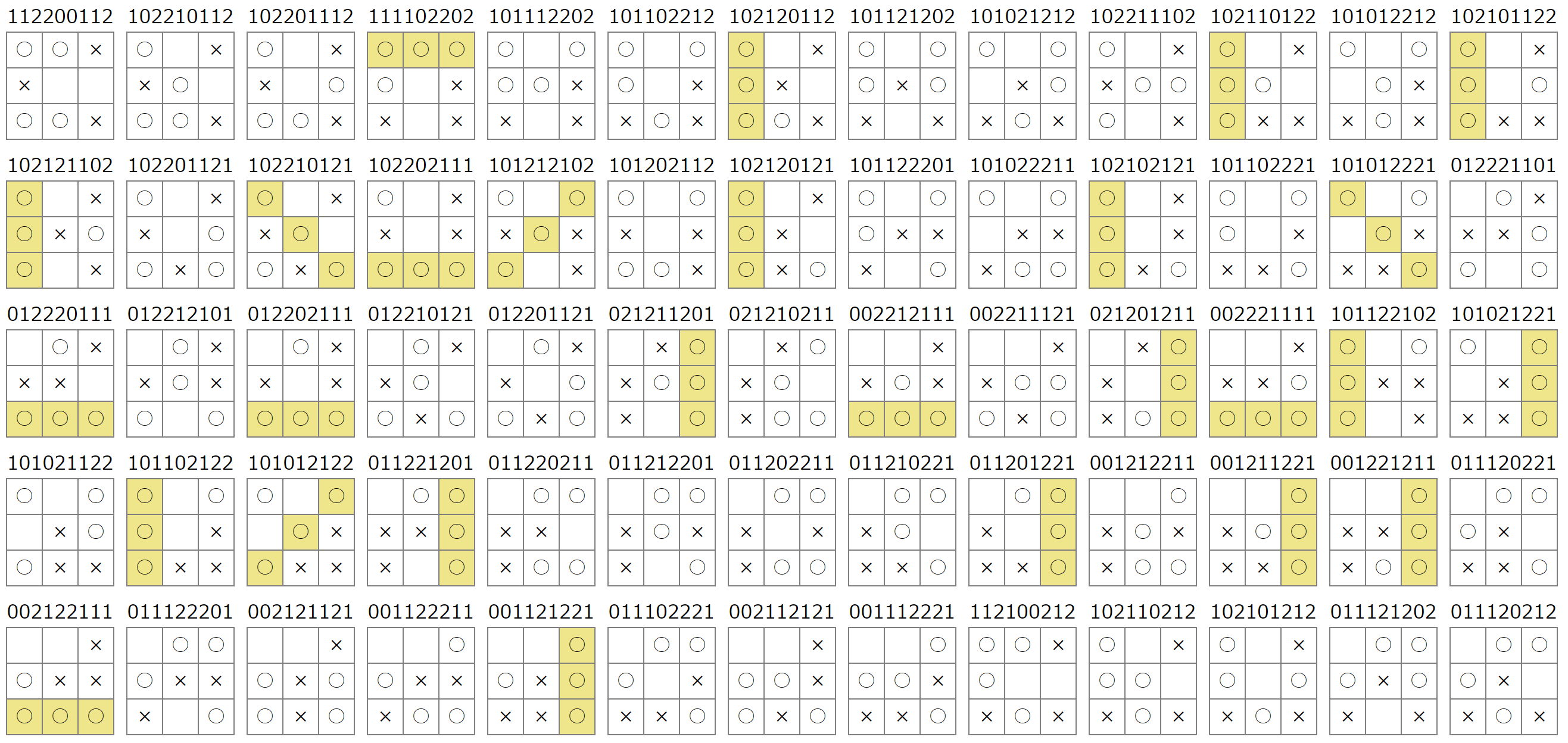
8手目で決勝:23パターン
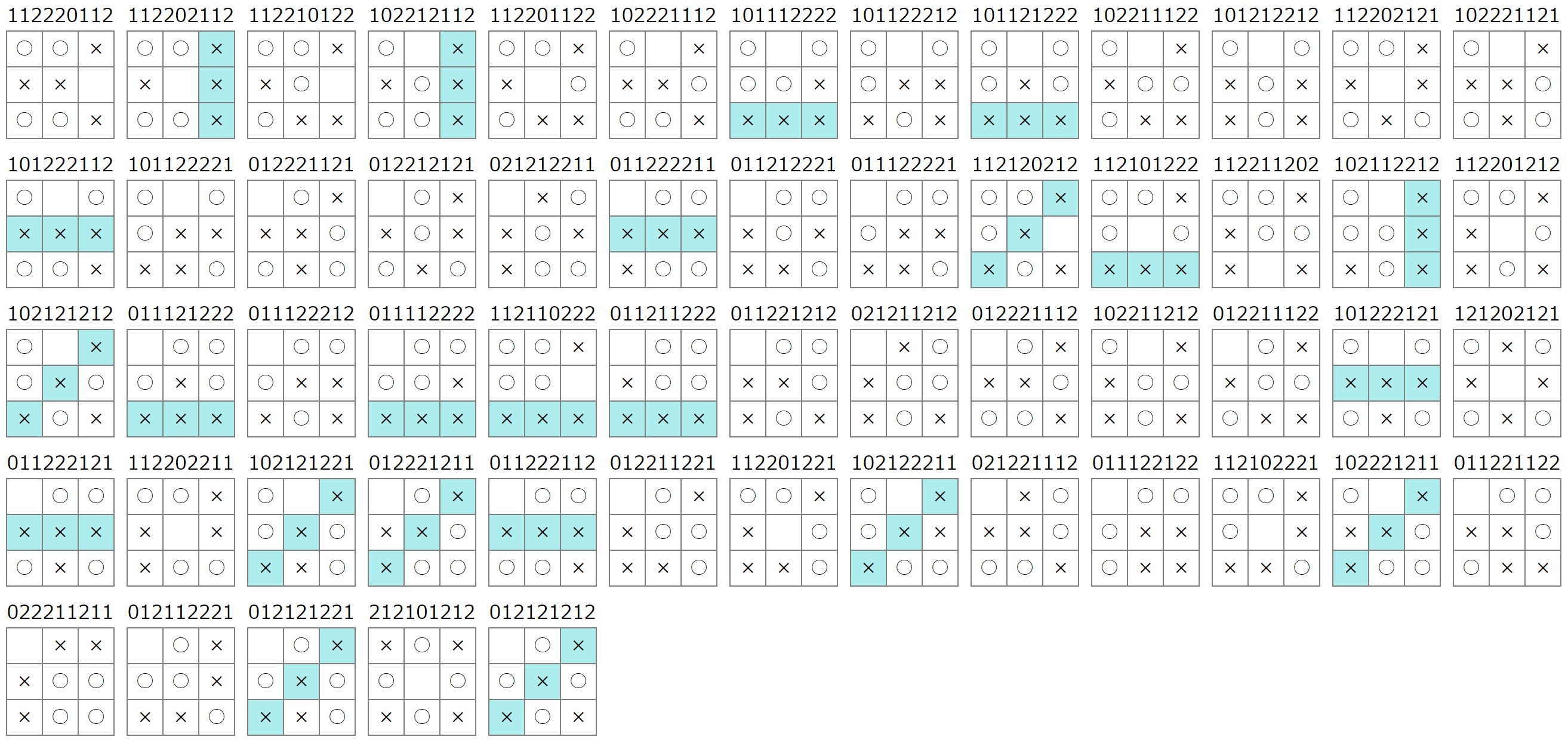
9手目で決勝:12パターン

決勝パターン合計:135(○:× = 91:44)
勝負なし:3、2ライン勝ち:6
手をランダムで決定した場合、勝負なしはたったの3パターンしか無いことは意外でした。
※ソースコードはこちら(HTMLファイル)